LC_最长公共前缀
LC最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例1:
输入:["flower","flow","flight"]
输出:[fl]
示例2:
输入:["dog","racecar","car"]
输出:""
解释:输入不存在公共前缀
说明:
所有人输入只包含小写字母a-z。
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
输入:["flower","flow","flight"]
输出:[fl]
输入:["dog","racecar","car"]
输出:""
解释:输入不存在公共前缀
所有人输入只包含小写字母a-z。
给定一个二叉树的 根节点
root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
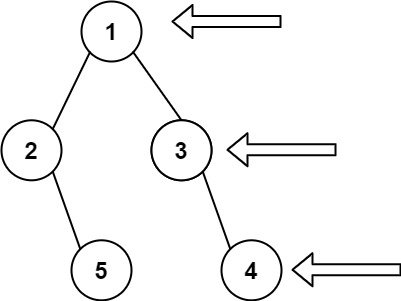
输入: [1,2,3,null,5,null,4] 输出: [1,3,4]
输入: [] 输出: []
[[toc]]
给定一个字符串 s 和一个字符串 t ,计算在 s
的子序列中 t 出现的个数。
字符串的一个 子序列
是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,"ACE" 是 "ABCDE" 的一个子序列,而 "AEC" 不是)
题目数据保证答案符合 32 位带符号整数范围。
输入:s = "rabbbit", t = "rabbit"
输出:3
解释:
如下图所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit
输入:s = "babgbag", t = "bag"
输出:5
解释:
如下图所示, 有 5 种可以从 s 中得到 "bag" 的方案,
babgbag
babgbag
babgbag
babgbag
babgbag
[[toc]] # 91. 解码方法
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
'A' -> "1"
'B' -> "2"
...
'Z' -> "26"
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,"11106" 可以映射为:
"AAJF" ,将消息分组为 (1 1 10 6) "KJF" ,将消息分组为 (11 10 6) 注意,消息不能分组为 (1 11 06) ,因为 "06" 不能映射为 "F" ,这是由于 "6" 和 "06" 在映射中并不等价。
给你一个只含数字的 非空 字符串 s ,请计算并返回 解码 方法的 总数 。
题目数据保证答案肯定是一个 32 位 的整数。
输入:s = "12"
输出:2
解释:它可以解码为 "AB"(1 2)或者 "L"(12)。
输入:s = "226"
输出:3
解释:它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。
[[toc]]
前面我们了解了前缀和
前缀和主要适用于原始数组不会被修改的情况下,频繁查询某个区间的累加和
差分数组主要适用于频繁对原始数组的某个区间的元素进行增减
比如我们给定一个数组nums
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| nums | 8 | 2 | 6 | 3 | 1 |
要求给区间nums[2..6]全部加1,再给nums[3..9]全部减3,再给nums[0..4]全部加2,最后问nums数组的值为多少?
常规做法就是每次在所给区间循环加上或者减去给定的值,时间复杂度为:O(m),效率比较低。
这时就需要用到差分数组,我们先对nums数组构造一个diff差分数组,diff[i] = nums[i] - nums[i-1]