148. 排序链表

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

示例

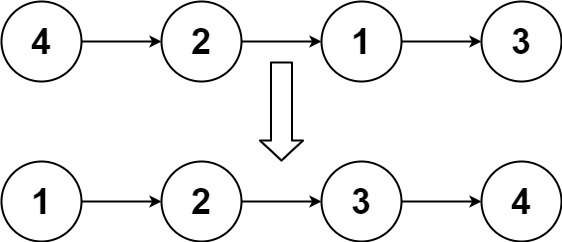
输入：head = [4,2,1,3]
输出：[1,2,3,4]

输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

输入：head = []
输出：[]

HJ77 火车进站

描述

给定一个正整数N代表火车数量，0 < N < 10，接下来输入火车入站的序列，一共N辆火车，每辆火车以数字1-9 编号，火车站只有一个方向进出，同时停靠在火车站的列车中，只有后进站的出站了，先进站的才能出站。

要求输出所有火车出站的方案，以字典序排序输出。

数据范围：1≤ n ≤10 1 ≤ n ≤10

进阶：时间复杂度：O(n!) ，空间复杂度：O(n)

输入描述：

第一行输入一个正整数N（0 < N <= 10），第二行包括N个正整数，范围为1到10。

输出描述：

输出以字典序从小到大排序的火车出站序列号，每个编号以空格隔开，每个输出序列换行，具体见sample。

这两个通配符是最常用的，其中点号「.」可以匹配任意一个字符，星号「*」可以让之前的那个字符重复任意次数（包括 0 次）。

比如说模式串".a*b"就可以匹配文本"zaaab"，也可以匹配"cb"；模式串"a..b"可以匹配文本"amnb"；而模式串".*"就比较牛逼了，它可以匹配任何文本。

题目会给我们输入两个字符串s和p，s代表文本，p代表模式串，请你判断模式串p是否可以匹配文本s。我们可以假设模式串只包含小写字母和上述两种通配符且一定合法，不会出现*a或者b**这种不合法的模式串，

总结自labuladong大神

前缀和技巧适用于快速、频繁地计算一个索引区间内的元素之和。

303. 区域和检索 - 数组不可变

给定一个整数数组 nums，处理以下类型的多个查询:

计算索引 left和right （包含 left 和 right）之间的 nums 元素的和 ，其中 left <= right 实现 NumArray 类：

• NumArray(int[] nums) 使用数组 nums 初始化对象
• int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的总和 ，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + ... + nums[right] )

示例：

输入：

["NumArray", "sumRange", "sumRange", "sumRange"]

[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]

输出：

[null, 1, -1, -3]

解释：

NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);

numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)

numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))

numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

描述

查找两个字符串a,b中的最长公共子串。若有多个，输出在较短串中最先出现的那个。

注：子串的定义：将一个字符串删去前缀和后缀（也可以不删）形成的字符串。请和“子序列”的概念分开！

数据范围：字符串长度1<= length<=30

进阶：时间复杂度：O(n^3) ，空间复杂度：O(n)

示例

输入：

abcdefghijklmnop abcsafjklmnopqrstuvw

输出：

jklmnop

对于子串问题，大部分都可以通过滑动窗口来解决。说起来滑动窗口的思路非常简单，就是维护一个窗口，不断滑动，然后更新答案。这个算法的时间复杂度为O(N)，比字符串暴力算法要高效多了，这里我们可以学习下labuladong大神的框架。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;
    
    int left = 0, right = 0;
    int valid = 0; 
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移（增大）窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/
        
        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移（缩小）窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

通过下面的一道题来深入了解下滑动窗口：

#HJ61 放苹果

描述

把m个同样的苹果放在n个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？

注意：如果有7个苹果和3个盘子，（5，1，1）和（1，5，1）被视为是同一种分法。

数据范围：0≤m≤10 0≤m≤10 ，1≤n≤10 1≤n≤10 。

示例：

输入：

7 3

输出：

8

#HJ43 迷宫问题

描述

定义一个二维数组 N*M ，如 5 × 5 数组下所示：

1
2
3
4
5
6
7

int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
}; 

它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的路线。入口点为[0,0],既第一格是可以走的路。

数据范围： 2≤n,m≤10 2≤*n*,*m*≤10， 输入的内容只包含 0≤val≤1 0≤*v**a**l*≤1

887. 鸡蛋掉落

给你k枚相同的鸡蛋，并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。

已知存在楼层 f ，满足0 <= f <= n ，任何从 高于 f 的楼层落下的鸡蛋都会碎，从 f 楼层或比它低的楼层落下的鸡蛋都不会破。

每次操作，你可以取一枚没有碎的鸡蛋并把它从任一楼层 x 扔下（满足 1 <= x <= n）。如果鸡蛋碎了，你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎，则可以在之后的操作中 重复使用 这枚鸡蛋。

请你计算并返回要确定f确切的值 的最小操作次数 是多少？

示例：

输入：k = 1, n = 2
输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，肯定能得出 f = 0 。
否则，鸡蛋从 2 楼掉落。如果它碎了，肯定能得出 f = 1 。
如果它没碎，那么肯定能得出 f = 2 。
因此，在最坏的情况下我们需要移动 2 次以确定 f 是多少。

#198. 打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。