109. 有序链表转换二叉搜索树

给定一个单链表的头节点 head，其中的元素 按升序排序 ，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。

示例：

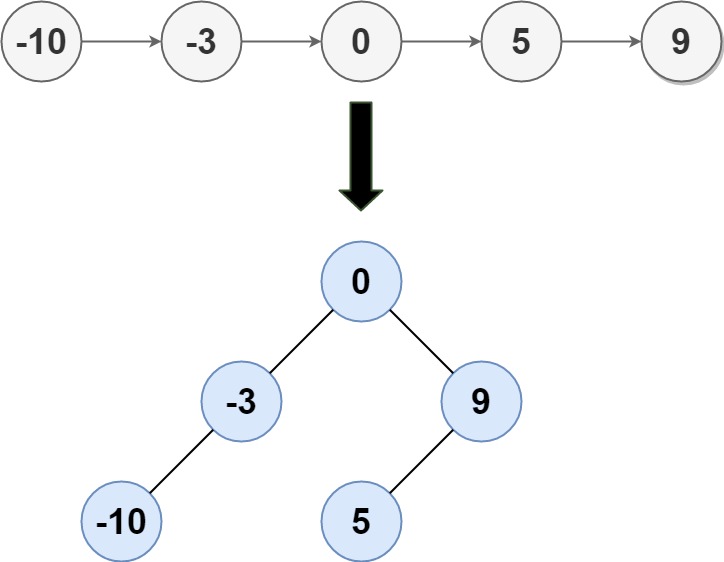
输入: head = [-10,-3,0,5,9]

输出: [0,-3,9,-10,null,5]

解释: 一个可能的答案是[0，-3,9，-10,null,5]，它表示所示的高度平衡的二叉搜索树。

思路：

方法一：通过快慢双指针找到链表中间节点

由于我们需要构造出平衡二叉树，那么我们第一步就是确定根结点，并且使根结点的左子树和右子树节点个数尽可能接近。这样左右子树的高度才能达到高度差的绝对值不超过1。

那么如何找到这样的根结点呢？理所当然我们想到找到链表的中心节点。

时间复杂度为O(nlogn)

空间复杂度为O(logn)

class Solution1 {
public: 
    TreeNode* sortedListToBST(ListNode* head){
        return build(head, nullptr);
    }
    // 把链表左闭右开区间[begin,end) 的节点构造成 BST
    TreeNode* build(ListNode *begin, ListNode *end){
        if(begin == end){
            return nullptr;
        }
        ListNode *mid = getMid(begin, end);
        TreeNode *root = new TreeNode(mid->val);
        root->left = build(begin, mid);
        root->right = build(mid->next, end);
        return root;
    }
    // 通过双指针获取链表左闭右开区间的中心结点
    ListNode* getMid(ListNode *begin, ListNode *end){
        ListNode *slow = begin, *fast = begin;
        while(fast != end && fast->next != end){
            slow = slow->next;
            fast = fast->next->next;
        }
        return slow;
    }
};

方法二：中序遍历

方法一中我们的时间都浪费在了查找中间节点上，我们每次获取链表的头结点O(1),它对应BST的最左子树的根结点

我们根据中序遍历原则，分别构建左子树，根结点，右子树

时间复杂度：O(n)

空间复杂度：O(logn)

class Solution {
public:
    ListNode *cur;
    TreeNode* sortedListToBST(ListNode* head) {
        int len = 0;
      	//计算链表长度
        for(ListNode *p = head; p != nullptr; p = p->next){
            len++;
        }
        cur = head;
        return inorderBuild(0, len - 1);
    }
    TreeNode* inorderBuild(int lo, int hi){
        if(lo > hi){
            return nullptr;
        }
        int mid = lo + (hi - lo) / 2;
        // 构造左子树
        TreeNode *leftTree = inorderBuild(lo, mid - 1);
        // 构造根结点
        TreeNode *root = new TreeNode(cur->val);
        cur = cur->next;
        // 构造右子树
        TreeNode *rightTree = inorderBuild(mid + 1, hi);
        // 将左右子树链接到根结点上
        root->left = leftTree;
        root->right = rightTree;
        return root;
    }
};