柱状图中最大的矩形

发表于 分类于 ， 阅读次数： Waline： 本文字数： 1.2k 阅读时长 ≈ 1 分钟

单调栈的具体思路可以看单调栈

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例

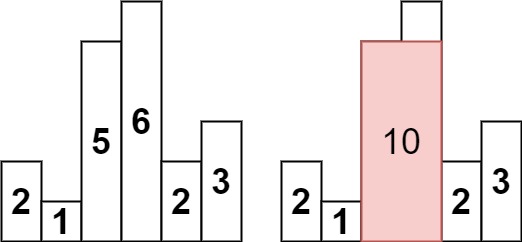
输入：heights = [2,1,5,6,2,3]

输出：10

解释：最大的矩形为图中红色区域，面积为 10

思路：

具体可以参考题解，讲得挺好的，这里我简单讲下思路。

我们在遍历的时候，需要记录的是下标，如果当前的高度比它之前的高度严格小于的时候，就可以直接确定之前的那个高的柱形的最大矩形的面积，为了确定这个最大矩形的左边界，我们还要找到第一个严格小于它的高度的矩形，向左回退的时候，其实就可以当中间这些柱形不存在一样。

为了方便计算，我们左右两边加上哨兵，作用就是：

  • 左边的柱形（第 1 个柱形）由于它一定比输入数组里任何一个元素小，它肯定不会出栈，因此栈一定不会为空；

  • 右边的柱形（第 2 个柱形）也正是因为它一定比输入数组里任何一个元素小，它会让所有输入数组里的元素出栈（第 1 个哨兵元素除外）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        if(heights.size() == 1) return heights[0];
        int area = 0;
        //插入哨兵
        heights.insert(heights.begin(), 0);
        heights.push_back(0);
        int n = heights.size();
        stack<int> st;
        st.push(0);
        
        for(int i = 1; i < n; i++){
            while(heights[i] < heights[st.top()]){
                //确定前一个高的柱形的最大矩阵高度
                int height = heights[st.top()];
                st.pop();
                int width = i - st.top() - 1;
                area = max(area, height * width);
            }
            st.push(i);
        }
        return area;
    }
};