Essential C++ 第五章 面向对象编程风格

发表于 分类于 ， 阅读次数： Waline： 本文字数： 13k 阅读时长 ≈ 12 分钟

第五章 面向对象编程风格

5.1 面向对象编程概念

面向对象编程概念的两项最主要特质是：继承和多态。前者使我们得以将一群相关的类组织起来，并让我们得以分享其间的共通数据和操作行为，后者让我们在这些类之上进行编程时，可以如同操作单一个体，而非互相独立的类，并赋予我们更多弹性来加入或移除任何特定类。

继承机制定义了父子关系。父类定义了所有子类共通的共有接口和私有实现。每个子类都可以增加或覆盖（override）继承而来的东西，以实现其自身独特的行为。

在C++中，父类被称为基类（base class），子类被称为派生类(derived class)。父类和子类之间的关系则称为继承体系。

抽象基类： 例如下面的LibMat，LibMat用来定义图书馆系统中所有馆藏的共通操作行为，包括check_in(),check_on(),due_data(),find()等等。LibMat并不代表图书馆借阅管理系统中实际存在的任何一个馆藏，仅仅是为了我们设计上的需要而存在。但事实上这个抽象十分关键。我们称之为"抽象基类"。

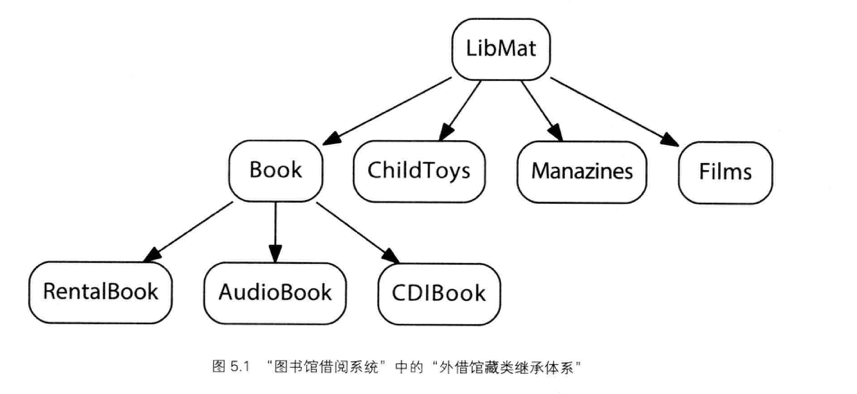
在面向对象应用程序时中，我们会间接利用「指向抽象基类」的指针或引用来操作系统中的各对象，而不是直接操作各个实际对象。这让我们得以在不更动旧友程序的前提下，加入或移除任何一个派生类。如：

1
2
3
4
5
6
7
8
9
10
11
void loan_check_in(LiMat &mat){
    //mat 实际上代表派生类的对象
    //诸如Book,RentalBook,Magazines等
    mat.check_in();

    if(mat.is_late())
        mat.assest_fine();
    
    if(mat.waiting_list())
        mat.notify_available();
}

我们的程序中并不存在LiMat对象，只有Book,RentalBook等类对象。

面向对象编程风格的第二个独特概念是多态： 让基类的指针或引用得以十分透明地指向其任何一个派生类的对象。以上述的loan_check_in()为例，mat总是指向（代表）LiMat的某个派生对象。但究竟是哪个？除非程序实际运行的当下，否则无法确定。而且，loan_check_in()的每次执行情况都可能不同。

动态绑定是面向对象编程风格的第三个独特概念。就是直到运行时，我们才能找出实际被调用的是哪个派生类的函数。

总结：

继承特性让我们得以定义一整群互有关联的类，并享有共通的接口，就像上述的各种图书馆藏。多态则让我们得以用一种与类型无关的方式来操作这些类对象。我们通过抽象基类的指针或引用来操作其共通接口，而实际执行起来的操作则需要等到运行时，依据指针或引用所指的实际对象的类型才能决定。多态和动态绑定的特性，只有在使用指针或引用时才能发挥。

5.2 漫游：面向对象编程思维

我们从LibMat排生出Book，再从Book派生出AudioBook。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <iostream>
using namespace std;

class LibMat{
public:
    //构造函数
    LibMat(){
        cout << "调用构造函数LibMat::LibMat()\n";
    }
    virtual ~LibMat(){
        cout << "调用析构函数LibMat::~LibMat()\n";
    }
    virtual void print() const{
        cout << "调用LibMat::print(),我是一个LibMat对象!\n";
    }
};

void print(const LibMat &mat){
    cout << "调用mat.print()\n";
    mat.print();
}

//继承LibMat
class Book :public LibMat{
public:
    //构造函数
    Book(const string &title, const string &author)
    :_title(title),_author(author)
    {
        cout << "调用构造函数Book::Book()\n";
    }
    virtual ~Book(){
        cout << "调用析构函数Book::~Book()\n";
    }
    virtual void print() const{
        cout << "调用Book::print()\n我是一个Book对象\n"
        << "我的名称是：" << _title << "我的作者是：" << _author << endl;
    }
protected:
    //protected的成员派生类都可以访问
    string _title;
    string _author;
};

//继承Book
class AudioBook :public Book{
public:
    //构造函数
    AudioBook(const string &title, const string &author, const string &narr)
    :Book(title,author), _narr(narr)
    {
        cout << "调用构造函数AudioBook::AudioBook\n";
    }
    //析构函数
    ~AudioBook(){
        cout << "调用AudioBook::print()\n" << "我是一个AudioBook对象!\n"
			<< "我的名称是：" << _title << "我的作者是" << _author
			<< "我的旁白是" << _narr << endl;
    }
protected:
    string _narr;
};

int main(){
    AudioBook ab("Esstential C++","候杰","KKKK");
    print(ab);
    return 0;
}

输出结果：

调用构造函数LibMat::LibMat()

调用构造函数Book::Book()

调用构造函数AudioBook::AudioBook

调用mat.print()

调用Book::print()

我是一个Book对象

我的名称是：Esstential C++我的作者是：候杰

调用AudioBook::print()

我是一个AudioBook对象!

我的名称是：Esstential C++我的作者是候杰我的旁白是KKKK

调用析构函数Book::~Book()

调用析构函数LibMat::~LibMat()

5.3 不带继承的多态

利用函数指针数组和枚举在某种程度上也能模拟多态，但是每次维护所需要的成本极大。

5.4 定义一个抽象基类

我们要为斐波那契数列设计一个共享的抽象基类，然后继承它。

定义抽象类的第一个步骤就是找出所有子类共通的操作行为。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class num_sequence{
public:
    //elem(pos): 返回 pos 位置上的元素
    //gen_elems(pos): 产生直到 pos 位置的所有元素
    //what_am_i(): 返回确切的数列类型
    //print(os): 将所有元素写入 os
    //check_integrity(pos): 检查 pos 是否为有效位置
    //max_elems(): 返回所支持的最大位置值
    int elem(int pos);
    void gen_elems(int pos);
    const char* what_am_i() const;
    ostream& print(ostream &os = cout) const;
    bool check_integrity(int pos);
    static int max_elems();
};

设计抽象基类的下一步，便是设法找出哪些操作行为与类型相关----也就是说有哪些操作行为必须根据不同的派生类而有不同的实现方式。这些操作行为应该成为整个类继承体系中的虚函数。

需要注意的是static修饰的函数无法被声明为虚函数

设计抽象基类的第三步，便是试着找出每个操作行为的访问层级。

  • 如果某个操作行为应该让一般程序都能访问，我们应该将它声明为public，例如elem(),max_elems(),what_am_i()。

  • 如果某个操作行为在基类之外不需要被用到，我们就将它声明为private。即使是该基类的派生类，亦无法访问基类中的private member。本例的所有操作都必须给派生类使用，所以我们不能把它们声明为private。

  • 第三种访问层级，是所谓的protected，这种层级的操作行为可让派生类访问，却不允许一般程序使用。例如check_integrity（）和gen_elems()都是派生类必须调用的，却不是一般程序会用到的。

下面就是重新修改后的num_sequenceclass定义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class num_sequence{
public:
    virtual ~num_sequence(){};
    virtual int elem(int pos) const = 0;        //返回 pos 位置上的元素
    virtual const char* what_am_i() const = 0;  //返回确切的数列类型
    static int max_elems(){                     //返回所支持的最大位置值
        return _max_elems;
    }
    virtual ostream& print(ostream &os = cout) const = 0;   //将所有元素写入 os
protected:
    virtual void gen_elems(int pos) const = 0;              //产生直到 pos 位置的所有元素
    bool check_integrity(int pos) const;                    //检查 pos 是否为有效位置
    const static int _max_elems = 1024;
};

每个虚函数，要么有定义，要么可设为“纯”虚函数------如果对于该类而言，这个虚函数并无实质意义的话，将虚函数赋值为0，意思便是令它成为一个纯虚函数。

1
virtual void gen_elems(int pos) = 0;

任何类如果有一个（或多个）纯虚函数，那么，由于其接口的不完整性，程序无法为它产生任何对象。这种类只能作为派生类的子对象使用，而且前提是这些派生类必须为所有虚函数提供确切的定义。

这里有几点要注意的点，由于static成员所有对象只有一份，所有类也只有一份，所以static成员函数没法声明成虚函数。

由于虚函数是运行的时候才决定要调用哪一个，所以我们在使用那个接口以前虚函数必须有定义，如果这个虚函数在基类中什么也不干的话可以设计成纯虚函数。

对于抽象基类，如果这个基类没有需要初始化的数据成员，那么就没必要给他写构造函数。

对于析构函数，最好不要在抽象基类中把他声明成纯虚函数。

以下为一个数列的抽象基类。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class num_sequence{
public:
    virtual ~num_sequence(){};
    virtual int elem(int pos) const = 0;        //返回 pos 位置上的元素
    virtual const char* what_am_i() const = 0;  //返回确切的数列类型
    static int max_elems(){                     //返回所支持的最大位置值
        return _max_elems;
    }
    virtual ostream& print(ostream &os = cout) const = 0;   //将所有元素写入 os
protected:
    virtual void gen_elems(int pos) const = 0;              //产生直到 pos 位置的所有元素
    bool check_integrity(int pos) const;                    //检查 pos 是否为有效位置
    const static int _max_elems = 1024;
};

bool num_sequence::check_integrity(int pos) const{
    if(pos <= 0 || pos > _max_elems){
        cerr << "!!位置非法\n";
        return false;
    }
    return true;
}

ostream& operator<<(ostream &os, const num_sequence &ns){
    return ns.print(os);
}

5.5 定义一个派生类

派生类由两部分组成：一是基类构成的子对象，二是派生类的部分。派生类的名称之后紧跟着冒号，关键字public，以及基类的名称。唯一的规则就是，类进行继承声明之前，其基类的定义必须已经存在。

1
2
3
4
5
6
#include "num_sequence.h"

class Fibonacci : public num_sequence{
public:
    //...
};

派生类由基类的非静态数据成员和派生类自己的特有部分组成。

派生类必须对从基类继承来的每个纯虚函数给出具体的实现。

Fibonacci class必须为其基类继承而来的每个纯虚函数提供对应的实现。除此之外，它还必须声明Fibonacciclass 专属的member。以下为Fibonacciclass 的定义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include "num_sequence.h"

class Fibonacci : public num_sequence{
public:
    Fibonacci(int len = 1, int beg_pos = 1)
    :_length(len), _beg_pos(beg_pos){}

    virtual int elem(int pos) const;
    virtual const char* what_am_i() const{
        return "Fibonacci";
    }
    virtual ostream& print(ostream &os = cout) const;
    int length() const{
        return _length;
    }
    int beg_pos() const{
        return _beg_pos;
    }
protected:
    virtual void gen_elems(int pos) const;
    int _length;
    int _beg_pos;
    static vector<int> _elems;
};

我们把没有把长度和起始位置，length()和beg_pos()设置为虚函数，因为它们并无基类所提供的实体可供覆盖。但这样的话我们也无法通过基类的指针或引用来访问。所以我们最好在基类中加入两个纯虚函数。

以下便是elem()的实现。派生类的虚函数必须精确吻合基类中的函数原型。在类之外对虚函数进行定义时，不必指明关键字virtual

1
2
3
4
5
6
7
8
9
10
int Fibonacci::elem(int pos) const{
    //不合法
    if(!check_integrity(pos)){
        return 0;
    }
    if(pos > _elems.size()){
        Fibonacci::gen_elems(pos);
    }
    return _elems[pos - 1];
}

一般来说，继承而来的public成员和protected成员，都可以视为派生类自身拥有的成员。基类的public member在派生类中同样是public，同样开发给派生类用户使用。基类的protected member在派生类中同样也是protected，同样只能给后续的派生类使用，无法给目前这个派生类的用户使用。基类的private member，则完全无法让派生类使用。

在返回pos位置上的元素前，我们会检查_elems拥有的元素是否足够。如果不够，elem()会调用gen_elems()，计算必要的元素并填入_elems。这个操作必须写成Fibonacci::gen_elems(pos)，因为我们很清楚我们想调用的究竟是哪一个gen_elems()，不必等到运行时才进行gen_elems()的解析操作。

下面我们实现gen_elems()和print()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//计算斐波那契数列元素
void Fibonacci::gen_elems(int pos) const{
    //pos = 0 和 pos = 1时，斐波那契为 1
    if(_elems.empty()){
        _elems.push_back(1);
        _elems.push_back(1);
    }
    if(_elems.size() <= pos){
        int ix = _elems.size();
        //后一个数等于前两个数之和
        int n_2 = _elems[ix - 2];
        int n_1 = _elems[ix - 1];

        for(; ix <= pos; ++ix){
            int elem = n_2 + n_1;
            _elems.push_back(elem);
            n_2 = n_1;
            n_1 = elem;
        }
    }
}

//输出
ostream& Fibonacci::print(ostream &os) const{
    //开始位置
    int elem_pos = _beg_pos - 1;
    //结束位置
    int end_pos = elem_pos + _length;
    //不够就计算
    if(end_pos > _elems.size()){
        Fibonacci::gen_elems(end_pos);
    }
    while(elem_pos < end_pos){
        os << _elems[elem_pos++]<< ' ';
    }
    return os;
}

我们把check_integrity()的功能改造一下，能够直接帮我们把填充数据那一步做了，给基类的check_integrity()函数改造一下：

1
2
3
4
5
6
7
8
9
10
bool num_sequence::check_integrity(int pos, int size) const{
    if(pos <= 0 || pos > _max_elems){
        cerr << "!!位置非法\n";
        return false;
    }
    if(pos > size){
        gen_elems(pos);
    }
    return true;
}

elem()

1
2
3
4
5
6
7
8
9
10
int Fibonacci::elem(int pos) const{
    //不合法
    if(!check_integrity(pos, _elems.size())){
        return 0;
    }
    if(pos > _elems.size()){
        Fibonacci::gen_elems(pos);
    }
    return _elems[pos - 1];
}

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#ifndef CIRCLE_H
#define CIRCLE_H

#include <iostream>
using namespace std;

class num_sequence{
public:
    virtual ~num_sequence(){};
    virtual int elem(int pos) const = 0;        //返回 pos 位置上的元素
    virtual const char* what_am_i() const = 0;  //返回确切的数列类型
    static int max_elems(){                     //返回所支持的最大位置值
        return _max_elems;
    }
    virtual ostream& print(ostream &os = cout) const = 0;   //将所有元素写入 os
protected:
    virtual void gen_elems(int pos) const = 0;              //产生直到 pos 位置的所有元素
    bool check_integrity(int pos, int size) const;                    //检查 pos 是否为有效位置
    const static int _max_elems = 1024;
};

bool num_sequence::check_integrity(int pos, int size) const{
    if(pos <= 0 || pos > _max_elems){
        cerr << "!!位置非法\n";
        return false;
    }
    if(pos > size){
        gen_elems(pos);
    }
    return true;
}

ostream& operator<<(ostream &os, const num_sequence &ns){
    return ns.print(os);
}

#endif
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include "num_sequence.h"
#include <vector>

class Fibonacci : public num_sequence{
public:
    Fibonacci(int len = 1, int beg_pos = 1)
    :_length(len), _beg_pos(beg_pos){}

    virtual int elem(int pos) const;
    virtual const char* what_am_i() const{
        return "Fibonacci";
    }
    virtual ostream& print(ostream &os = cout) const;
    int length() const{
        return _length;
    }
    int beg_pos() const{
        return _beg_pos;
    }
protected:
    virtual void gen_elems(int pos) const;
    int _length;
    int _beg_pos;
    static vector<int> _elems;
};
/*
返回 pos 位置上的元素前，检查拥有的元素是否足够，不够就通过
gen_elems()构造。
*/
int Fibonacci::elem(int pos) const{
    //不合法
    if(!check_integrity(pos, _elems.size())){
        return 0;
    }
    if(pos > _elems.size()){
        Fibonacci::gen_elems(pos);
    }
    return _elems[pos - 1];
}

//计算斐波那契数列元素
void Fibonacci::gen_elems(int pos) const{
    //pos = 0 和 pos = 1时，斐波那契为 1
    if(_elems.empty()){
        _elems.push_back(1);
        _elems.push_back(1);
    }
    if(_elems.size() <= pos){
        int ix = _elems.size();
        //后一个数等于前两个数之和
        int n_2 = _elems[ix - 2];
        int n_1 = _elems[ix - 1];

        for(; ix <= pos; ++ix){
            int elem = n_2 + n_1;
            _elems.push_back(elem);
            n_2 = n_1;
            n_1 = elem;
        }
    }
}

//输出
ostream& Fibonacci::print(ostream &os) const{
    //开始位置
    int elem_pos = _beg_pos - 1;
    //结束位置
    int end_pos = elem_pos + _length;
    //不够就计算
    if(end_pos > _elems.size()){
        Fibonacci::gen_elems(end_pos);
    }
    while(elem_pos < end_pos){
        os << _elems[elem_pos++]<< ' ';
    }
    return os;
}

int main(){
    Fibonacci fib;
    cout << "fib: 1 到 1 的斐波那契数列 " << fib << endl;
    Fibonacci fib2(16);
    cout << "fib2: 1 到 16 的斐波那契数列 " << fib2 << endl;
    Fibonacci fib3(8, 12);
    cout << "fib3: 8 到 12 的斐波那契数列 " << fib2 << endl;
    return 0;
}