112_路径总和

发表于 分类于 ， 阅读次数： Waline： 本文字数： 2.1k 阅读时长 ≈ 2 分钟

112. 路径总和

给你二叉树的根节点 root和一个表示目标和的整数 targetSum。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum。如果存在，返回 true；否则，返回 false。

叶子节点 是指没有子节点的节点。

示例：

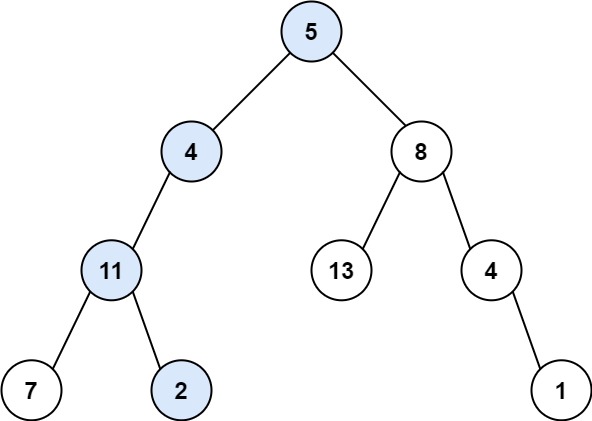
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22

输出：true

解释：等于目标和的根节点到叶节点路径如上图所示。

思路：

方法一：DFS

我们分解为小问题，递归解决

假设为左子树，那么可以表示为

1
hasPathSum(root->left, targetSum - root->val);

右子树同理

时间复杂度：O(n) 空间复杂度：O(h) h 为树高

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root == nullptr){
            return false;
        }
        if(root->left== nullptr && root->right == nullptr && root->val == targetSum){
            return true;
        }
        return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);
    }
};

方法二：BFS

我们定义两个队列，分别存储当前节点和该节点的值，分别相加，直到达到叶子节点后判断相加的和和targetSum是否相等

时间复杂度：O(n)

空间复杂度：O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution1 {
public:
    bool hasPathSum(TreeNode* root, int targetSum){
        if(root == nullptr){
            return false;
        }
        queue<TreeNode*> que_node;
        queue<int> que_val;
        que_node.push(root);
        que_val.push(root->val);
        while(!que_node.empty()){
            TreeNode *now = que_node.front();
            int temp = que_val.front();
            que_node.pop();
            que_val.pop();
            // 为叶子结点
            if(now->left == nullptr && now->right == nullptr){
                if(temp == targetSum){
                    return true;
                }
                continue;
            }
            if(now->left != nullptr){
                que_node.push(now->left);
                que_val.push(now->left->val + temp);
            }
            if(now->right != nullptr){
                que_node.push(now->right);
                que_val.push(now->right->val + temp);
            }
        }
        return false;
    }
};