最长有效括号

发表于 分类于 阅读次数： Waline： 本文字数： 2.9k 阅读时长 ≈ 3 分钟

32. 最长有效括号

给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

示例：

输入：s = "(()"

输出：2

解释：最长有效括号子串是 "()"

思路：

方法一：栈

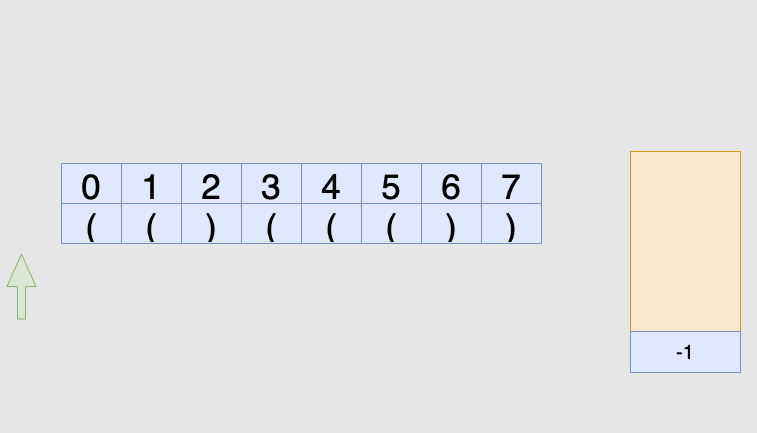
具体做法是我们始终保持栈底元素为当前已经遍历过的元素中「最后一个没有被匹配的右括号的下标」，

这样的做法主要是考虑了边界条件的处理，栈里其他元素维护左括号的下标：

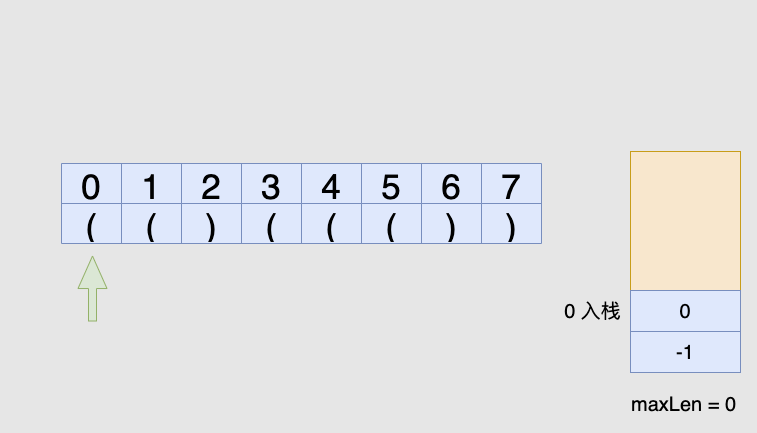
  • 对于遇到的每个'('，我们将它的下标放入栈中

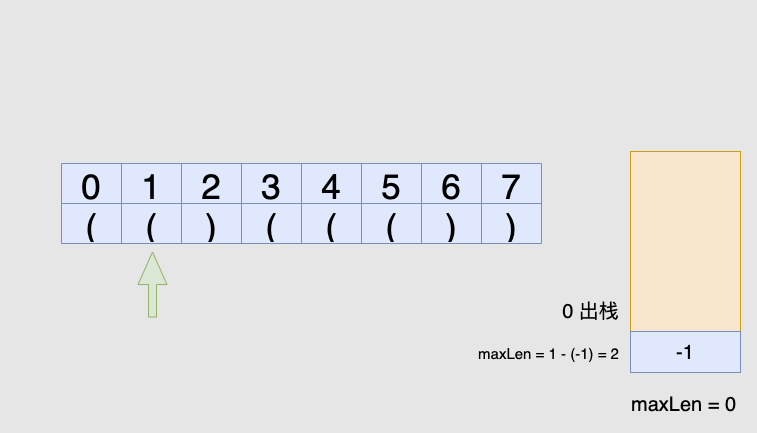
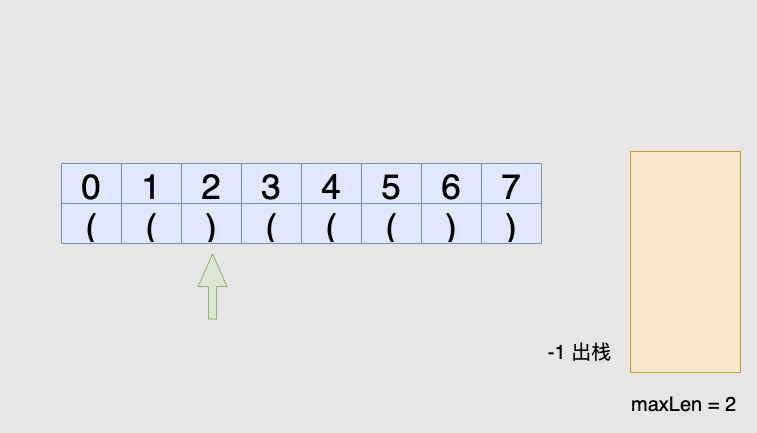
  • 对于遇到的每个')',我们先弹出栈顶元素表示匹配了当前右括号：

    • 如果栈为空，说明当前的右括号为没有被匹配的右括号，我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」

    • 如果栈不为空，当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度」

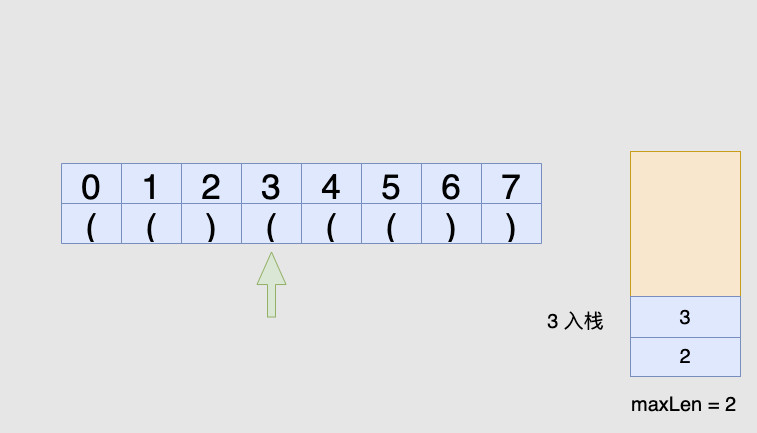
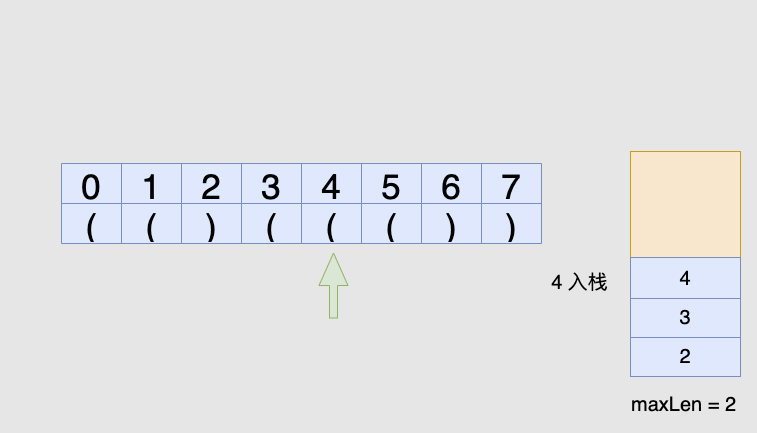
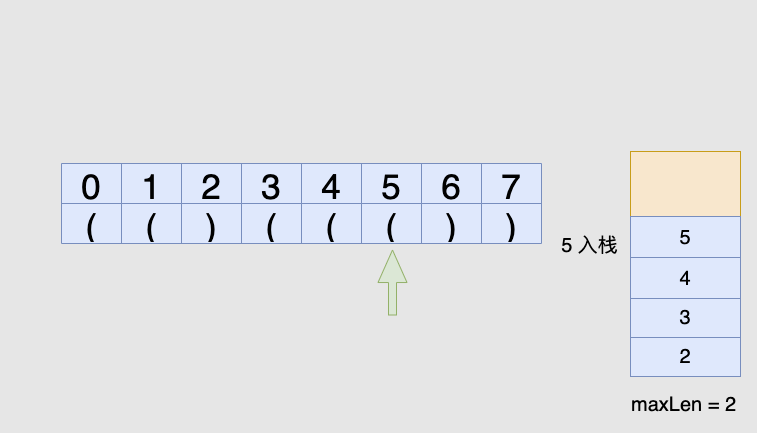
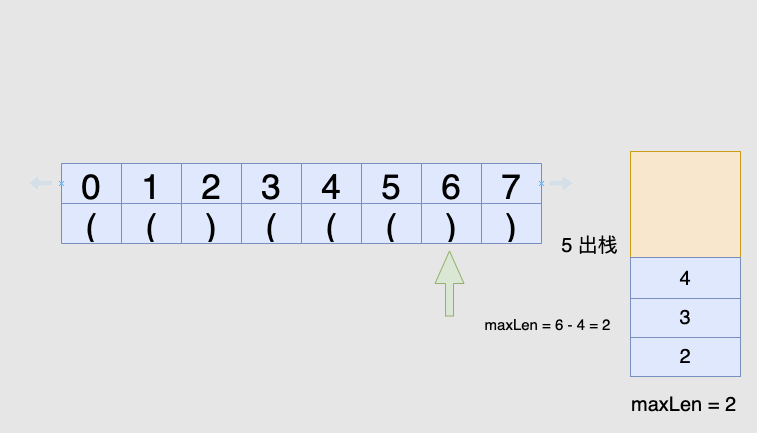
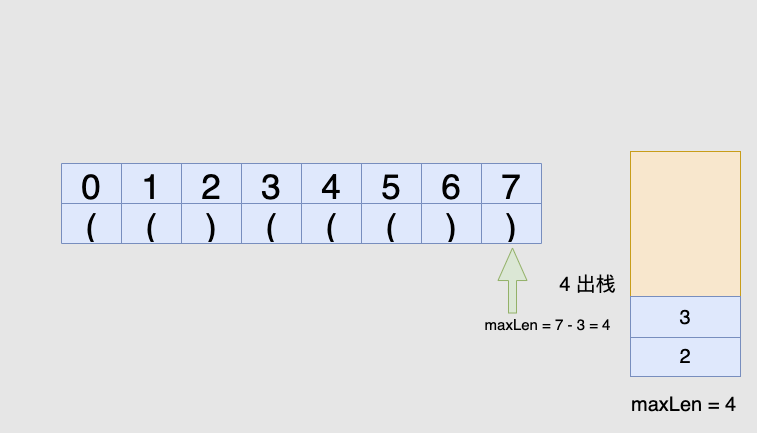
到此我们可以写出如下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int longestValidParentheses(string s) {
        int maxLen = 0;
        stack<int> st;
        st.push(-1);
        for(int i = 0; i < s.size(); i++){
            if(s[i] == '('){
                st.push(i);
            }else{
                st.pop();
                if(st.empty()){
                    //栈为空，则把这个右括号入栈
                    st.push(i);
                }else{
                    maxLen = max(maxLen, i - st.top());
                }
            }
        }
        return maxLen;
    }
};

方法二：动态规划

首先，我们定义一个 dp数组，其中第 i 个元素表示以下标为 i 的字符结尾的最长有效子字符串的长度。

我们先看第i个位置，这个位置的元素s[i]可能有如下两种情况：

  • s[i]=='('：

    这时，s[i]无法和之前的元素组成有效的括号对，所以dp[i] = 0

  • s[i] == ')':

    这时需要看其前面元素来判断是否有有效括号对。

    • 情况一：s[i - 1] == '(':

      即s[i]和s[i-1]组成一对有效括号，有效括号新增长度 2 ，i位置的最长有效括号长度为其之前两个位置的最长括号长度加上当前新增的 2

      即：

      dp[i] = dp[i - 2] + 2

    • 情况二：s[i - 1] == ')':

      这种情况下，如果前面有和s[i]组成有效括号对的字符，即形如((...))，就要求s[i - 1]位置必然是有效的括号对，否则s[i]无法和前面组成有效括号对。

      这时，我们只需要找到和s[i]配对的括号位置，并判断其是否配对。

      和其配对的位置为：i - 1 - dp[i-1]。因为如果s[i]为有效的话s[i-1]也必然有效，而s[i-1]表示的是以i-1为结尾的最长有效子字符串的长度，所以和s[i]配对的括号位置为:i - 1 - dp[i - 1]。

      • 如果s[i - 1 - dp[i-1]] == '('：

        有效括号长度新增 2， 即dp[i] = dp[i - 1] + 2

      这里需要注意的是，我们还需要加上dp[i - 2 - dp[i - 1]]这个位置的最长有效子字符串的长度，（也就是和s[i]配对的括号的前一个的最长有效子字符串长度）

      即：

      dp[i] = dp[i] + dp[i - 2 + dp[i - 1]]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    int longestValidParentheses(string s) {
        int n = s.size();
        vector<int> dp(n, 0);
        int res = 0;
        for(int i = 1; i < n; i++){
            if(s[i] == ')'){
                //匹配
                if(s[i - 1] == '('){
                    dp[i] = 2;
                    //判断前面是不是匹配
                    if(i - 2 >= 0){
                        dp[i] = dp[i] + dp[i - 2];
                    }
                }else if(dp[i - 1] >= 0){//代表s[i]前面的匹配了
                    //(i - 1) - dp[i - 1]这个含义就是当前下标减去当前下标对应最长有效括号长度,
                    //也就是当前索引下的对应最长有效括号的前一个下标
                    if((i - 1 - dp[i - 1]) >= 0 && s[i - 1 - dp[i - 1]] == '('){
                        dp[i] = dp[i - 1] + 2;
                       //加上和s[i]配对的括号的前一个字符的最长有效子字符串长度
                        if(i - 2 - dp[i - 1] >= 0){
                            dp[i] = dp[i] + dp[i - 2 - dp[i - 1]];
                        }
                    }
                }
            }
            res = max(res, dp[i]);
        }
        return res;
    }
};