最近公共祖先问题

发表于 分类于 ， 阅读次数： Waline： 本文字数： 2.7k 阅读时长 ≈ 2 分钟

236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x是 p、q的祖先且 x的深度尽可能大（一个节点也可以是它自己的祖先）。

示例：

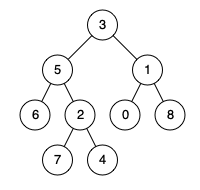
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1

输出：3

解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4

输出：5

解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

思路：

祖先的定义： 若节点 p在节点 root的左（右）子树中，或 p = root，则称root 是p 的祖先。

最近公共祖先的定义： 设节点root 为节点 p,q的某公共祖先，若其左子节点 root->left和右子节点root->right都不是p,q 的公共祖先，则称 root是 “最近的公共祖先” 。

根据以上定义：若root是p，q的最近公共祖先

  • p和q在root的左或右子树中。
  • p= root，q在root的左或右子树中
  • q = root，p在root的左或右子树中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        return find(root, p->val, q->val);
    }
    TreeNode* find(TreeNode *root, int val1, int val2){
        if(root == nullptr) return nullptr;
        //前序位置,如果p,q为根节点，则公共祖先为根节点
        if(root->val == val1 || root->val == val2){
            return root;
        }
        TreeNode *left = find(root->left, val1, val2);
        TreeNode *right = find(root->right, val1, val2);
        //如果p,q为在单独一边，则去那边找
        if(left == nullptr) return right;
        if(right == nullptr) return left;

        //后序位置，p,q在两边
        if(left != nullptr && right != nullptr){
            //当前节点为 LCA 节点
            return root;
        }
        return nullptr;
    }
};

235. 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x是 p、q的祖先且 x的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例；

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8

输出: 6

解释: 节点 2 和节点 8 的最近公共祖先是 6。

思路：

用上面的方法可以做出来，但是没有用到二叉搜索树左小右大的性质，效率比较低。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        int val1 = min(p->val, q->val);
        int val2 = max(p->val, q->val);
        return find(root, val1, val2);
    }
    TreeNode* find(TreeNode *root, int val1, int val2){
        if(root == nullptr) return nullptr;
        //比最大的大，去左边找
        if(root->val > val2){
            return find(root->left, val1, val2);
        }
        //比最小的小，去右边找
        if(root->val < val1){
            return find(root->right, val1, val2);
        }
        return root;
    }
};