最小路径和

发表于 分类于 ， 阅读次数： Waline： 本文字数： 2.2k 阅读时长 ≈ 2 分钟

64. 最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例：

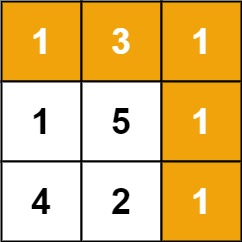
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]

输出：7

解释：因为路径 1→3→1→1→1 的总和最小。

思路：

我们想计算从D达到B的最小路径和，那我们就要解决如何才到到达B，因为只能向下或者向右移动一步，所以B

只能是从A或者C过来的，那么我们如何确定是从A过来的，而不是从C过来的，难道是因为A比c小吗？

当然不是，因为从D走到A的最小路径和为6，也就是上面橙色的部分，而从D走到C的最小路径和为8(1->1->4->2)，所以一定是从A走到B

这样我们就把「从D走到B的最小路径和」这个问题转换为了「从D走到A的最小路径和」和「从D走到C的最小路径和」,这样就可以得出状态转移方程

1
min(dp(i - 1, j), dp(i, j - 1)) + nums[i][j]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<vector<int> > memo;
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        if(m == 0) return 0;
        memo.resize(m, vector<int>(n, -1));
        return dp(grid, m - 1, n - 1);
    }
    int dp(vector<vector<int> >& grid, int x, int y){
        int m = grid.size(), n = grid[0].size();
        //base case
        if(x == 0 && y == 0){
            return grid[0][0];
        }
        if(x < 0 || y < 0){
            //如果索引出界，返回一个很大的值，保证在取 min 的时候不会取到
            return INT_MAX;
        }
        if(memo[x][y] != -1){
            return memo[x][y];
        }
      	//状态转移方程
        memo[x][y] = min(dp(grid, x - 1, y), dp(grid, x, y - 1)) + grid[x][y];
        return memo[x][y];
    }
};

我们借用了一个备忘录来处理重叠子问题。

时间和空间复杂度都为O(MN)。

迭代：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        if(m == 0) return 0;
        vector<vector<int> > dp(m, vector<int>(n, 0));

        dp[0][0] = grid[0][0];
        //计算最左边
        for(int i = 1; i < m; i++){
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        //计算最上边
        for(int j = 1; j < n; j++){
            dp[0][j] = dp[0][ j - 1] + grid[0][j];
        }

        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[m - 1][n - 1];
    }
};