问题背景
当下,我们每个人都有自己的亲感,但你能保证认识你所有的亲戚吗?如何确定一个陌生人是否是你的亲威呢?
如果有这样一个前提:拥有相同祖先的两个人是亲威。那么并查集就可以帮助我们判断某个陌生人是否是我们的亲戚。
通俗地讲一个故事:儿个家族进行宴会,但是家族音遍长寿,所以人数众多由于长时间的分离以及年龄的增长,这些人逐渐忘掉了自己的亲人,只记得自己的爸爸是谁了,而最长者(称为「祖先」)的父亲已经去世,他具知道自己是祖先。为了确定自己是哪个家族,他们想出了个办法,只要问自己的爸爸是不是祖先,一层一层的向上问,直到问到祖先。如果要判断两人是否在同一家族,只要看两人的祖先是不是同一人就可以了。
并查集应用
- ”边带权“并查集与“扩展域”并查集
- 判断图是否连通
- 最小生成树 Kruskal 算法
- 最近公共祖先LCA
并查集定义:
并查集是一种可以动态维护若干个不重叠的集合,并支持合并和查询的树形数据结构。
主要有以下两个基本操作:
- find,查询一个==元素==属于哪一个集合。
- merge,把两个集合合并为一个集合。
ps: 元素的表现形式是多样的,但最终会抽象为数字
如何表示一个集合?
第一种:”代表元“
法,每个集合选择一个固定的元素,树形结构中自然会想到树根作为该颗树的代表。
第二种:定义一个数组fa[]表示某个元素的父亲节点,特别地,根节点的父亲节点是自身(需要初始化)。

如何合并两个集合?
集合 a 的代表元是 a, fa[a] = a,集合 b 的代表元是
b,fa[b] = b
现在让集合 a 的父亲变为
b,使fa[a] = b,从而实现合并两个集合的操作。

这里我们具体问题具体分析,这里只是讲一下思想,方便了解。
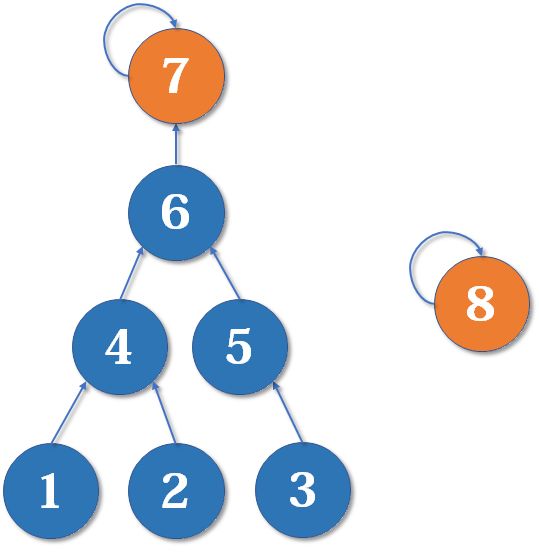
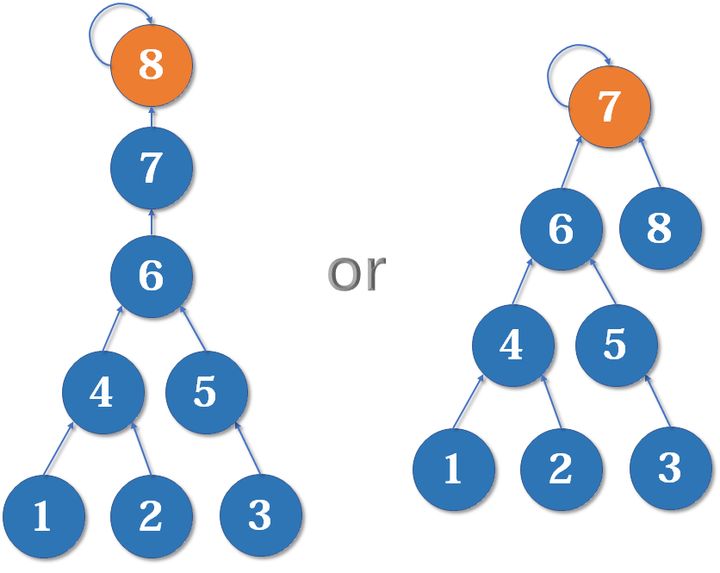
在合并时,我们按秩合并:==“秩” =
树的深度或者集合的大小,把元素少的集合合并到元素多的集合上。==
路径压缩
集合中如果要查寻节点4,5的集合代表元,要向上搜索很多次,效率低。所以需要考虑路径压缩,在查询find的过程中,让集合中的每一个元素的父亲都变为根节点。
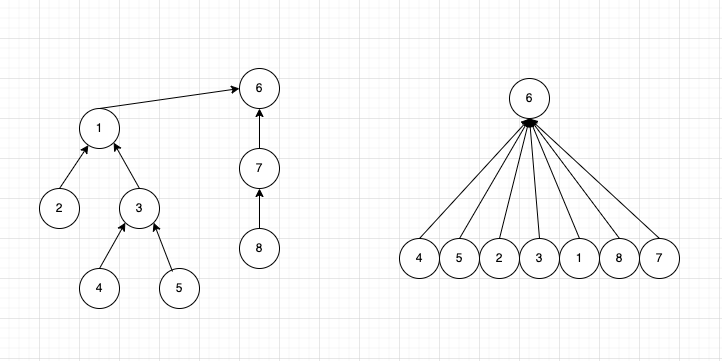
例如我们按照DFS来路径压缩。
不使用了路径压缩
1
2
3
4
5
6
7
|
int find(int x){
if(x == fa[x])
return x
else
return find(fa[x]);
}
|
使用路径压缩
1
2
3
4
5
6
|
int find(int x){
if(x != fa[x])
fa[x] = find(fa[x]);
return fa[x];
}
|
如何实现merge()函数
1
2
3
4
5
| void merge(int x, int y){
x = find(x);
y = find(y);
fa[x] = y;
}
|
初始化init()
1
2
3
4
5
| void init(int n){
for(int i = 0; i < n; i++){
fa[i] = i;
}
}
|
例题
题目背景
若某个家族人员过于庞大,要判断两个是否是亲戚,确实还很不容易,现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
题目描述
规定:x 和 y 是亲戚,y 和 z 是亲戚,那么 x 和 z 也是亲戚。如果 x,y
是亲戚,那么 x 的亲戚都是 y的亲戚,y 的亲戚也都是 x 的亲戚。
输入格式
第一行:三个整数 n , m p,(n,m,p≤5000),分别表示有 n
个人,m个亲戚关系,询问 p 对亲戚关系。
以下 m 行:每行两个数 \[M_i,M_j, 1 ≤
M_i,M_j ≤ N \],表示 \[M_i\]和
\[M_j\]具有亲戚关系。
接下来 p行:每行两个数 \[p_i,p_j\],询问 \[p_i\]和 \[p_j\]是否具有亲戚关系。
输出格式
p 行,每行一个 Yes 或 No。表示第
ii 个询问的答案为“具有”或“不具有”亲戚关系。
输入 #1
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6
输出 #1
Yes
Yes
No
思路:
典型的并查集,我们可以注意到描述中说的,x 和 y 是亲戚,y 和 z
是亲戚,那么 x 和 z
也是亲戚。这表示了具有传递性,要具体问题具体分析。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef vector<int> vi;
const int N = 1e5 + 10;
int fa[N];
int n,m,p;
int find(int x){
if(x != fa[x]){
fa[x] = find(fa[x]);
}
return fa[x];
}
void merge(int x, int y){
x = find(x);
y = find(y);
fa[x] = y;
}
void init(){
for(int i = 1; i <= n; i++){
fa[i] = i;
}
}
int main(){
cin >> n >> m >> p;
init();
while(m--){
int x, y;
cin >> x >> y;
merge(x,y);
}
while(p--){
int x, y;
cin >> x >> y;
if(find(x) == find(y)){
cout << "Yes\n";
}else{
cout <<"No\n";
}
}
return 0;
}
|
给你一个 m x n 的矩阵 board ,由若干字符
'X' 和 'O' ,找到所有被 'X'
围绕的区域,并将这些区域里所有的 'O' 用 'X'
填充。
###示例:
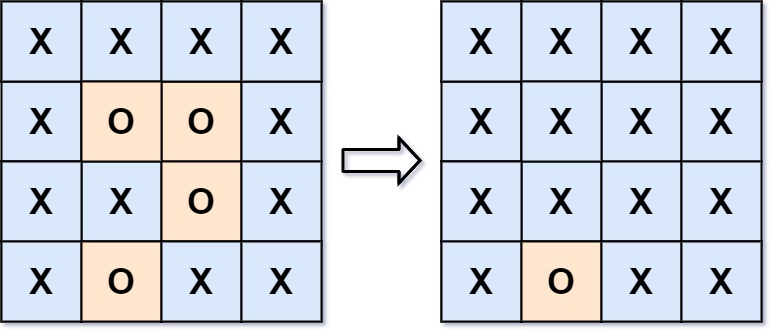
输入:board =
[["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O'
都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O'
最终都会被填充为
'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
思路:
常规方法就是DFS,从边界开始搜,和前面的岛屿问题类似。具体可以看一下写的岛屿部分。
这里直接给出代码,我们具体将并查集做法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| class Solution {
public:
void solve(vector<vector<char>>& board) {
int m = board.size(), n = board[0].size();
if(m == 0) return;
for(int i = 0; i < n; i++){
dfs(board, 0, i);
dfs(board, m - 1, i);
}
for(int i = 0; i < m; i++){
dfs(board, i, 0);
dfs(board, i, n - 1);
}
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(board[i][j] == 'A'){
board[i][j] = 'O';
}else if(board[i][j] == 'O'){
board[i][j] = 'X';
}
}
}
}
void dfs(vector<vector<char> >& board, int x, int y){
int m = board.size(), n = board[0].size();
if(x < 0 || x >= m || y < 0 || y >= n) return;
if(board[x][y] != 'O') return;
board[x][y] = 'A';
dfs(board, x + 1, y);
dfs(board, x - 1, y);
dfs(board, x, y + 1);
dfs(board, x, y - 1);
}
};
|
并查集就是定义一个节点,把边界的O和这个根节点连通,

然后再遍历整个 board,那些和 dummy 不连通的
O 就是被围绕的区域,需要被替换。
这里需要用到把二维数组映射为一维数组,(x,y) = x * n + y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| class Solution {
public:
int m, n;
vector<int> fa;
void init(int len){
fa.resize(len);
for(int i = 0; i < len; i++){
fa[i] = i;
}
}
int find(int x){
if(x != fa[x])
fa[x] = find(fa[x]);
return fa[x];
}
void to_union(int x, int y){
x = find(x);
y = find(y);
fa[x] = y;
}
void solve(vector<vector<char> >& board) {
m = board.size(), n = board[0].size();
init(n * m + 1);
int dummy = m * n;
for(int i = 0; i < m; i++){
if(board[i][0] == 'O'){
to_union(i * n, dummy);
}
if(board[i][n - 1] == 'O'){
to_union(i * n + n - 1, dummy);
}
}
for(int i = 0; i < n; i++){
if(board[0][i] == 'O'){
to_union(i, dummy);
}
if(board[m - 1][i] == 'O'){
to_union(n * (m - 1) + i, dummy);
}
}
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
for(int i = 1; i < m - 1; i++){
for(int j = 1; j < n - 1; j++){
if(board[i][j] == 'O'){
for(int k = 0; k < 4; k++){
int x = i + dx[k];
int y = j + dy[k];
if(board[x][y] == 'O'){
to_union(x * n + y, i * n + j);
}
}
}
}
}
for(int i = 1; i < m - 1; i++){
for(int j = 1; j < n - 1; j++){
if(find(dummy) != find(i * n + j)){
board[i][j] = 'X';
}
}
}
}
};
|






