给你一个整数 n ,按字典序返回范围 [1, n]
内所有整数。
你必须设计一个时间复杂度为 O(n) 且使用 O(1)
额外空间的算法。
示例:
输入:n = 13
输出:[1,10,11,12,13,2,3,4,5,6,7,8,9]
思路:
440
方法一:DFS
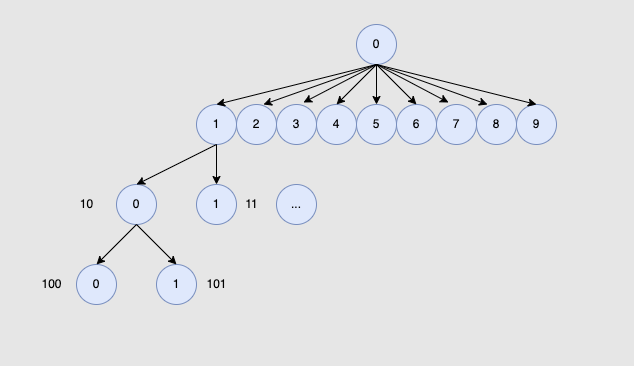
我们可以发现求字典序就是一棵树,我们从第二层开始递归遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
vector<int> lexicalOrder(int n) {
vector<int> res;
for(int i = 1; i <= 9; i++){
dfs(res, i, n);
}
return res;
}
void dfs(vector<int>& res, int k, int n){
if(k > n) return;
res.push_back(k);
for(int i = 0; i <= 9; i++){
dfs(res, k * 10 + i, n);
}
}
};
|
- 时间复杂度:本质上在搜索一棵节点数量为 n
的多阶树(形态类似于字典树),复杂度为 O(n)
- 空间复杂度:忽略递归带来的额外空间开销,复杂度为 O(1)
方法二:迭代
递归具有额外的空间开销,为了实现严格的 O(1)
空间,我们需要使用「迭代」来实现 DFS。
共有 n 个数需要被处理,假设当前处理到的数为
j,根据字典序规则,在满足条件的前提下,我们优先在 j 的后面添加 0(即 j *
10 < n 满足),否则我们考虑将上一位回退并进行加一操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
vector<int> lexicalOrder(int n) {
vector<int> res;
for(int i = 0, j = 1; i < n; i++){
res.push_back(j);
if(j * 10 <= n){
j *= 10;
}else{
while(j % 10 == 9 || j + 1 > n){
j /= 10;
}
j++;
}
}
return res;
}
};
|
