二叉搜索树BST

发表于 2022-08-16 分类于算法，二叉搜索树阅读次数： Waline：本文字数： 11k 阅读时长 ≈ 10 分钟

前面我们讲了二叉树，二叉搜索树(BST)就是特殊的二叉树而已。

首先，BST性质：

对于BST的每个节点node，左子树节点的值都比node的值小，右子树节点的值都比node的值大。
对于BST的每一个节点node，它的左子树和右子树都是BST
BST的中序遍历是升序。

二叉搜索树并不算难，但是基于BST的数据结构有二叉平衡树(AVL)，红黑树等等，还有B+树，线段树等结构都是基于BST的思想来设计的。

二叉搜索树上的基本操作所花费的时间与这棵树的高度成正比。基本操作的运行时间为O(lgN)

对于特性三，我们输入一颗BST树，可以通过中序遍历把BST中每个节点的值升序打印出来。

void traverse(TreeNode *root){
    if(root == nullptr) return;
    traverse(root->left);
    //中序遍历位置
    cout << root->val;
    traverse(root->right);
}

1. 寻找第K大的元素

230. 二叉搜索树中第K小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

示例：

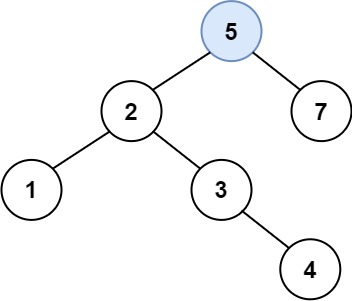
输入：root = [3,1,4,null,2], k = 1

输出：1

结构：

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

思路：

中序遍历，我们先遍历左子树，通过一个计数器cnt来计算是第几小的数，当cnt == k时结束

class Solution {
public:
    int res = 0;
    int cnt = 0;//记录当前排名
    int kthSmallest(TreeNode* root, int k) {
        //BST 中序遍历是升序
        inorder(root, k);
        return res;
    }
    void inorder(TreeNode* root, int k){
        if(root == nullptr) return;

        inorder(root->left, k);
        cnt++;
        if(cnt == k){
            res = root->val;
            return;
        }
        inorder(root->right, k);
    }
};

538. 把二叉搜索树转换为累加树

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node的新值等于原树中大于或等于 node.val的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。节点的右子树仅包含键大于节点键的节点。左右子树也必须是二叉搜索树。

示例：

思路：

先遍历右子树，然后值相加。

class Solution {
public:
    int sum = 0;
    TreeNode* convertBST(TreeNode* root) {
        //BST 中序遍历是升序,反过来先遍历右子树再遍历左子树就是降序
        if(root == nullptr) return nullptr;
        convertBST(root->right);
        root->val = root->val + sum;
        sum = root->val;
        convertBST(root->left);
        return root;
    }
};

2. 二叉搜索树的搜索，插入，删除

一般操作

void BST(TreeNode *root, int target) {
    if (root->val == target)
    //找到⽬标，做点什么
    if(root->val > target){
        BST(root->left, target)
    }
    if(root->val < target){
        BST(root->right, target)
    }
}

700. 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root和一个整数值 val。

你需要在 BST中找到节点值等于 val的节点。返回以该节点为根的子树。如果节点不存在，则返回 null。

示例：

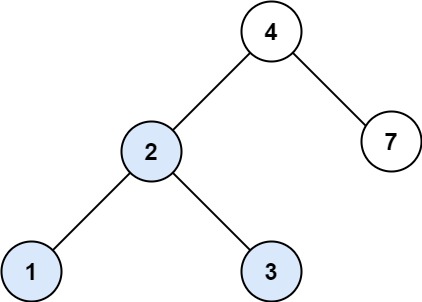
输入：root = [4,2,7,1,3], val = 2

输出：[2,1,3]

思路：

用BST的第一个特性，节点比左子树大，比右子树小。

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        //base case
        if(root == nullptr) return nullptr;

        //  去左边找
        if(root->val > val){
            return searchBST(root->left, val);
        }
        //去右边找
        if(root->val < val){
            return searchBST(root->right, val);
        }
        return root;
    }
};

701. 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回 任意有效的结果。

示例：

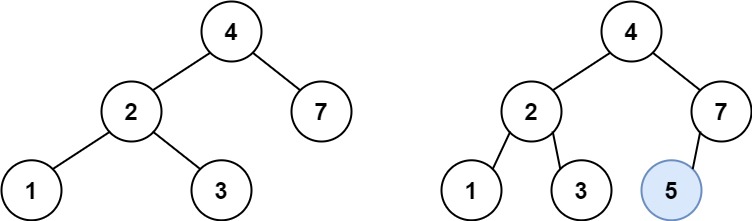
输入：root = [4,2,7,1,3], val = 5

输出：[4,2,7,1,3,5]

解释：另一个满足题目要求可以通过的树是：

思路：

插入有多种情况，最简单的就是在叶子节点插入，总可以找到这样一个节点。另一种需要我们重构二叉搜索树。

我们先采用简单的方法。

找到要插入的最后一个节点，构造新节点，判断要插入节点和当前节点的大小关系，如果比当前节点大，就插到右孩子处，反之，左孩子。

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if(root == nullptr){
            return new TreeNode(val);
        }
        if(root->val > val){
            root->left = insertIntoBST(root->left, val);
        }
        if(root->val < val){
            root->right = insertIntoBST(root->right, val);
        }
        return root;
    }
};

在讲删除之前，我们首先需要了解下如何判断二叉树是不是二叉搜索树。

定义：

BST中任意一个节点的左子树所有节点的值都小于该节点的值，右子树所有节点的值都大于该节点的值。
BST中任意一个节点的左右子树都是BST。

第二点是我们经常忽略的。我们需要找出左子树的最大的元素值，还有右子树的最小元素值去和当前节点比较，当前节点大于左子树的最大元素，小于右子树的最小元素，这才是合法的二叉搜索树。

98. 验证二叉搜索树

给你一个二叉树的根节点 root，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。

节点的右子树只包含大于当前节点的数。

所有左子树和右子树自身必须也是二叉搜索树。

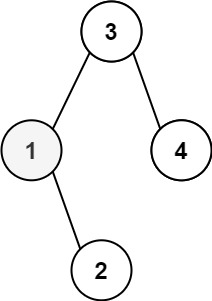
###示例：

输入：root = [2,1,3]

输出：true

思路：

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        return isValidBST(root, nullptr, nullptr);
    }
    bool isValidBST(TreeNode* root, TreeNode* min, TreeNode* max){
        //base case
        if(root == nullptr) return true;
        //若root->val 不符合 max 和 min 的限制，说明不是合法的 BST
        if(min != nullptr && root->val <= min->val) return false;
        if(max != nullptr && root->val >= max->val) return false;
        //限定左子树的最大值为 root->val 右子树的最小值为 root->val
        return isValidBST(root->left, min, root) 
            && isValidBST(root->right, root, max);
    }
};

450. 删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root和一个值 key，删除二叉搜索树中的 key对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；如果找到了，删除它。

示例：

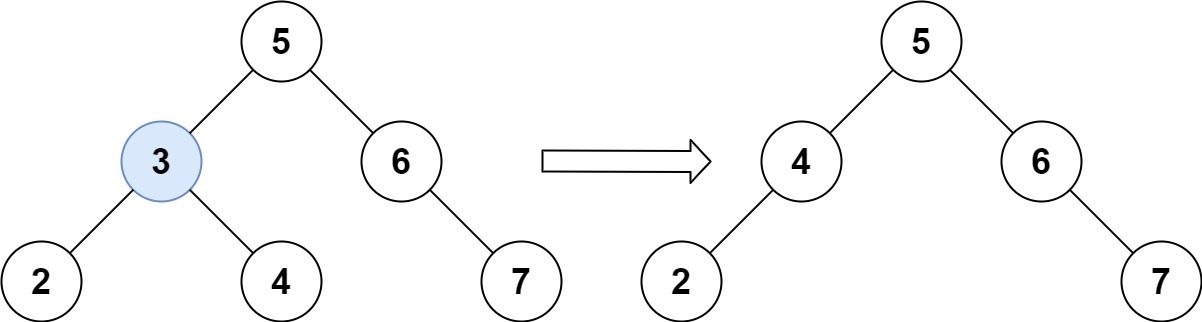
思路：

我们首先先找到这个节点，然后再去修改。

查找的话和我们前面的搜索一样

void BST(TreeNode *root, int target) {
    if (root->val == target)
    //找到⽬标
    if(root->val > target){
        BST(root->left, target)
    }
    if(root->val < target){
        BST(root->right, target)
    }
}

找到目标节点后，比如说节点A，如何删除这个节点呢？因为删除节点的同时不能破坏BST的性质。一共有3种情况：

情况一：A恰好是末端叶子节点。两个子节点都为空，那么我们可以直接删除

1
2
3

if(root->left == nullptr && root->right == nullptr){
  return nullptr;
}

情况二：A只有一个非空字节点，那么它要让这个孩子接替自己的位置

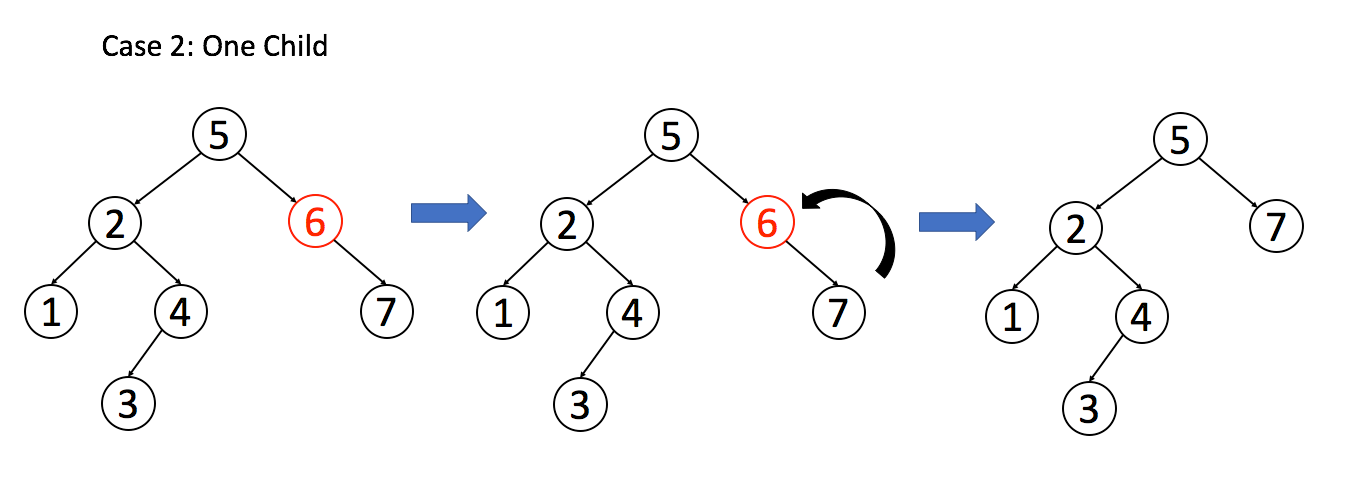
1 2	if(root->left == nullptr) return root->right; if(root->right == nullptr) return root->left;

情况三：A有两个子节点，为了不破坏BST的性质，A必须找到左子树中最大的那个节点或者右子树中最小的那个节点来接替自己。这里我们选择第二种。

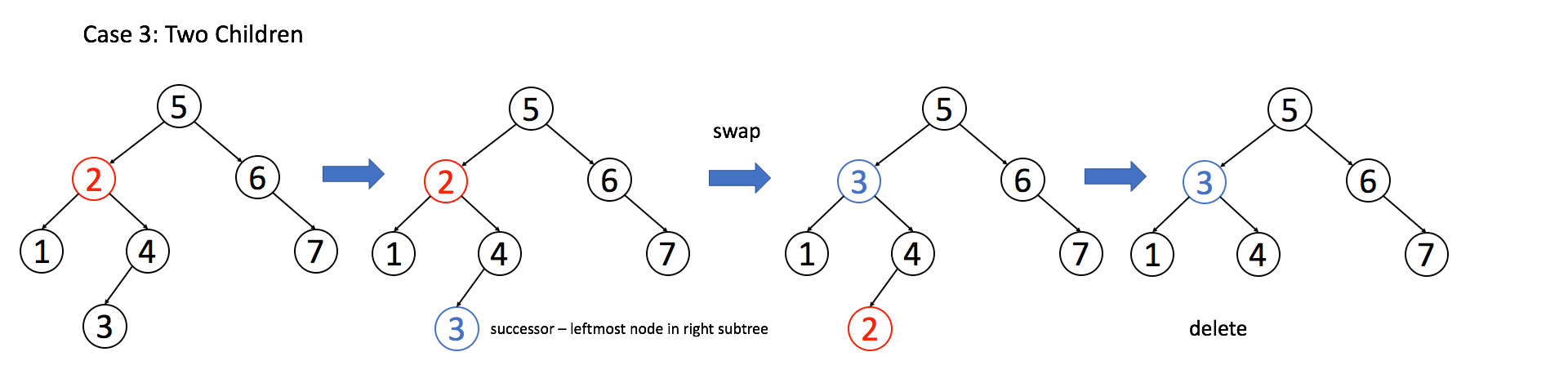
if(root->left != nullptr && root->right != nullptr){
  //找到右子树的最小节点
  TreeNode *minNode = getMin(root->right);
  //把 root 改成 minNode
  root->val = minNode->val;
  //删除 minNode
  root->right = deleteNode(root->right, minNode->val);
}

完整代码如下:

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        // base case
        if(root == nullptr) return nullptr;

        //和root节点比较,如果key比根节点大，我们就去右边寻找，否则左边
        if(root->val == key){
            //1,左右孩子都为空，或者一边为空
            if(root->left == nullptr) return root->right;
            if(root->right == nullptr) return root->left;
            //2,两边都不为空，我们可以直接把右孩子的最小节点代替父亲节点
            //获得右子树的最小节点
            TreeNode* minNode = getMin(root->right);
            //删除右子树大最小节点
            root->right = deleteNode(root->right, minNode->val);
            //用右子树最小的节点替换 root 节点
            minNode->left = root->left;
            minNode->right = root->right;
            root = minNode;
        }else if(root->val > key){//去左边找
            root->left = deleteNode(root->left, key);
        }else if(root->val < key){//去右边找
            root->right = deleteNode(root->right, key);
        }
        return root;
    }
    TreeNode* getMin(TreeNode* node){
        //bst 最左边的就是最小的节点
        while(node->left != nullptr) node = node->left;
        return node;
    }
};

3. 构造篇

96. 不同的二叉搜索树

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例：

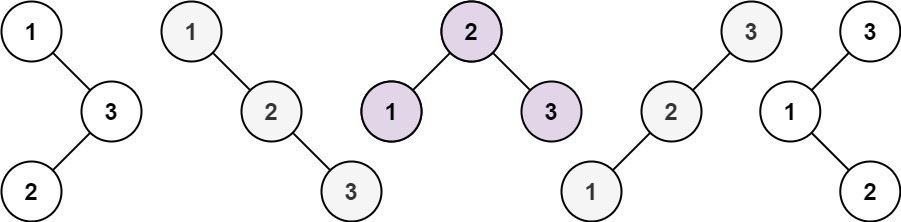
输入：n = 3

输出：5

思路：

例如我们输入：n = 5，也就是说用{1,2,3,4,5}这些数字去构造BST。

首先，根节点有5种情况，因为每个数字都可以作为根节点。

比如我们固定3作为根节点，这个前提下能有几种不同的BST呢？

根据 BST 的特性，根节点的左子树都比根节点的值小，右子树的值都比根节点的值大。

所以如果固定3作为根节点，左子树节点就是{1,2}的组合，右子树就是{4,5}的组合。

左子树的组合数和右子树的组合数乘积就是3作为根节点时的 BST 个数。

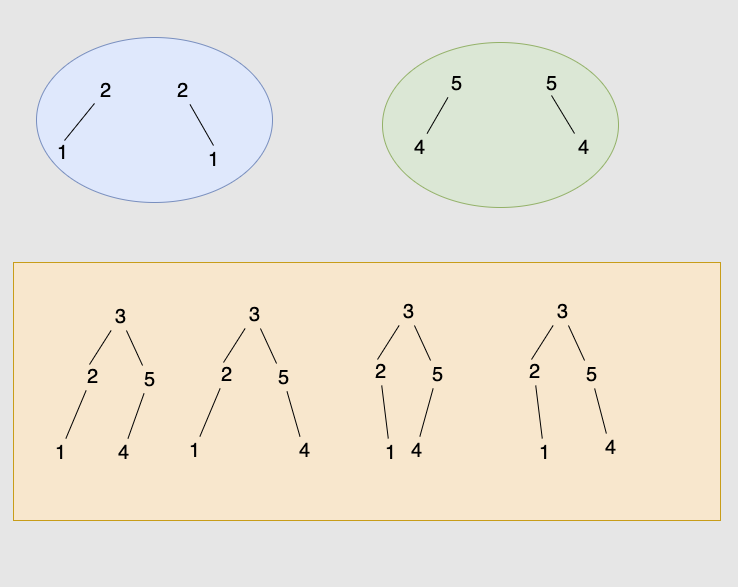
一共有2*2 = 4种,组合问题。

我们这是说了3为根节点这一种特殊情况，其实其他的节点也是一样的。

那你可能会问，我们可以一眼看出{1,2}和{4,5}有几种组合，但是怎么让算法进行计算呢？

我们只需要递归就可以了，我们可以写这样一个函数：

class Solution {
public:
    vector<vector<int> > memo;
    int numTrees(int n) {
        memo.resize(n + 1,vector<int>(n + 1,-1));
        //计算闭区间 [1,n] 组成的 BST 个数
        return count(1,n);
    }
    ////计算闭区间 [1,n] 组成的 BST 个数
    int count(int lo, int hi){
        //base case
        if(lo > hi) return 1;
        //避免重复计算
        if(memo[lo][hi] != -1){
            return memo[lo][hi];
        }
        int res = 0;
        for(int i = lo; i <= hi; i++){
            // i 的值作为根节点 root
            int left = count(lo, i - 1);
            int right = count(i + 1, hi);
            // 左右子树的组合数乘积是 BST 的总数
            res += left * right;
        }
        memo[lo][hi] = res;
        return res;
    }
};

注意 base case，显然当lo > hi闭区间[lo, hi]肯定是个空区间，也就对应着空节点 nullptr，虽然是空节点，但是也是一种情况，所以要返回 1而不能返回 0。

方法二：卡特兰数

令h(0)=1,h(1)=1，catalan数满足递推式。h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)。也就是说，如果能把公式化成上面这种形式的数，就是卡特兰数。

通项公式:

\[ C_n = \frac{1}{n + 1}C^{n}_{2n} = C^{n}_{2n} - C^{n-1}_{2n} \] 假设 n个节点存在二叉排序树的个数是G (n)，令f(i)为以i 为根的二叉搜索树的个数，则 \[ G(n) = f(1) + f(2) + f(3) + ... + f(n) \] 当i为根节点的时候，其左子树个数为i-1个，右子树为n - i则： \[ f(i) = G(i-1)*G(n-i) \] 综上可以得到卡特兰数： \[ G(n) = G(0) * G(n-1) + G(1) * G(n-2) + ... + G(n-1)*G(0) \]

代码如下：

class Solution {
public:
    int numTrees(int n) {
        vector<int> G(n + 1, 0);
        G[0] = 1;
        G[1] = 1;

        for(int i = 2; i <= n; i++){
            for(int j = 1; j <= i; j++){
                G[i] += G[j - 1] * G[i - j];
            }
        }
        return G[n];
    }
};

95. 不同的二叉搜索树 II

给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

示例：

输入：n = 3

输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

思路：

明白了上道题构造合法 BST 的方法，这道题的思路也是一样的：

1、穷举root节点的所有可能。

2、递归构造出左右子树的所有合法 BST。

3、给root节点穷举所有左右子树的组合。

class Solution {
public:
    vector<TreeNode*> generateTrees(int n) {
        if(n == 0) return {};
        //构造闭区间为 [1,n] 组成的BST
        return build(1,n);
    }
    vector<TreeNode*> build(int lo, int hi){
        vector<TreeNode*> res;
        //base case
        if(lo > hi){
            res.push_back(nullptr);
            return res;
        }
        // 1,穷举 root 节点的所有可能
        for(int i = lo; i <= hi; i++){
            // 2,递归构造出左右子树的所有合法 BST
            vector<TreeNode*> leftTree = build(lo, i - 1);
            vector<TreeNode*> rightTree = build(i + 1, hi);
            // 3,给 root 节点穷举所有左右子树的组合
            for(TreeNode* left : leftTree){
                for(TreeNode* right : rightTree){
                    // i 作为根节点 root 的值
                    TreeNode* root = new TreeNode(i);
                    root->left = left;
                    root->right = right;
                    res.push_back(root);
                }
            }
        }
        return res;
    }
};