LC最长回文子串

发表于 分类于 ， 阅读次数： Waline： 本文字数： 5.3k 阅读时长 ≈ 5 分钟

最长回文子串

给定一个字符 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例1:

输入:

babad

输出：

bab

注意：

"aba"也是一个有效答案。

示例2:

输入：

cbbd

：

bb

方法一：暴力匹配（Brute Force）

  • 根据回文子串的定义，枚举所有长度大于等于2的子串，依次判断它们是否是回文
  • 在具体实现时，可以只针对大于“当前得到的最长回文子串长度”的子串进行“回文判断”
  • 在记录最长回文子串时，只记录当前子串的起始位置和子串长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
private:
	bool valid(string s,int left, int right){
		//验证子串s[left,right]是否为回文串
		while(left <= right){
			if(s[left] != s[right]){
				return false;
			}
			left++;
			right--;
		}
		return true;
	}
public:
    string longestPalindrome(string s) {
    	//特判
    	int len = s.size();
    	if(len < 2){
    		return s;
    	}

    	int maxLen = 1;
    	string res = s.substr(0,1);

    	//枚举所有长度大于等于2的子串
    	for(int i = 0; i < len - 1; i++){
    		for(int j = i + 1; j < len; j++){
    			if(j - i + 1 > maxLen && valid(s,i,j)){
    				maxLen = j - i + 1;
    				res = s.substr(i,maxLen);
    			}
    		}
    	}
    	return res;
    }
};

方法二：动态规划

1，思考状态（重点）
  • 状态的定义，先尝试（题目问什么，就把什么设置为状态）；
  • 然后思考「状态如何转移」，如果「状态转移方程」不容易得到，尝试修改定义，目的依然是为了方便得到「状态转移方程」。

状态转移方程是原始问题的不同规模的子问题的联系。即大问题的最优解如何由小问题的最优解得到的。

2，思考状态转移方程（核心，难点）
  • 常见的推到技巧是：分类讨论。即：对状态空间进行分类；
  • 「动态规划」方法依然是「空间换时间」思想的体现，常见的解决问题的过程很像在「填表」。
3，思考初始化

初始化是非常重要的，一步错，步步错。初始化状态一定要设置对，才可能得到正确的结果。

  • 角度1: 直接从状态的语义出发。
  • 角度2: 如果状态的语义不好思考，就考虑「状态转移方程」的边界需要什么样初始化的条件；
  • 角度3: 从「状态转移方程」的下标看是否需要多设置一行，一列表示「哨兵」，这样可以避免一些特殊情况的讨论。
4，思考输出

有些时候是最后一个状态，有些时候可能会综合之前所有计算过的状态。

5，思考优化空间（也可以叫表格复用）
  • 经典的「优化空间」的典型问题是「0-1」背包问题和「完全背包」问题。

分析

对于这道题来说，我们从回文串的定义展开讨论：

  • 如果一个字符串的头尾两个字符不相等，那么这两个字符串一定不是回文串；

  • 如果一个字符串的头尾两个字符相等，才有必要继续判断下去

    ​ 1，如果里面的子串是回文，整体就是回文

    ​ 2，如果里面的子串不是回文，整体就不是回文

综上： 在头尾字符相等的情况，里面的回文性质决定了整个子串的回文性质这就是状态转移。因此可以把「状态」定义为原字符串的一个子串是否是回文子串。

第1步：定义状态

dp[ i ][ j ]表示子串s[ i , j ]是否为回文子串，这里可以取到s[ i ]和s[ j ]。

第2步：思考状态转移方程

根据我们前面的分析（头尾字符是否相等），可以得到：

dp[i][j] = (s[i] == s[j]) and dp[i + 1][j - 1]

这里需要注意：

  • 「动态规划」事实上是在填一张二维表格，由于构成子串，因此 [^ i] 和 [^ j] 的关系

是[^i < = j] ，因此，只需要填这张表格对角线以上的部分。

  • 看到[^ dp[i + 1, j - 1] ] 就得考虑边界情况。

边界条件是：表达式 [^ [i + 1, j - 1]] 不构成区间，即长度严格小于 2，即[^ j - 1 - (i + 1) + 1 < 2 ]，整理得[^ j - i < 3]。

这个结论很显然：j - i < 3 等价于 j - i + 1 < 4，即当子串 s[i..j] 的长度等于 2 或者等于 3 的时候，其实只需要判断一下头尾两个字符是否相等就可以直接下结论了。

  • 如果子串 s[i + 1..j - 1] 只有 1 个字符，即去掉两头，剩下中间部分只有 1个字符，显然是回文；

  • 如果子串 s[i + 1..j - 1] 为空串，那么子串 s[i, j] 一定是回文子串。

因此，在 s[i] == s[j] 成立和 j - i < 3 的前提下，直接可以下结论，dp[ i ][ j ] = true，否则才执行状态转移。

##### 第3步：考虑初始化

初始化的时候，单个字符一定是回文串，因此把对角线先初始化为 true，即 dp[i][i] = true 。

事实上，初始化的部分都可以省去。因为只有一个字符的时候一定是回文，dp[ i ][ i ] 根本不会被其它状态值所参考。

第4步：考虑输出

只要一得到 dp[ i ] [ j ] = true，就记录子串的长度和起始位置，没有必要截取，这是因为截取字符串也要消耗性能，记录此时的回文子串的「起始位置」和「回文长度」即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    string longestPalindrome(string s) {
    	//特判
    	int len = s.size();
    	if(len < 2){
    		return s;
    	}
    	int maxLen = 1;
    	int begin = 0;

    	//dp[i][j]表示s[i,j]是否是回文串
    	vector<vector<bool>> dp(len,vector<bool>(len));
    	for(int j = 1; j < len; j++){
    		for(int i = 0; i < j; i++){
    			if(s[i] != s[j]){
    				dp[i][j] = false;
    				continue;
    			}else if(j - i < 3){
    				dp[i][j] = true;
    			}else{
    				dp[i][j] = dp[i + 1][j - 1];
    			}
    			if(dp[i][j] && (j - i + 1 > maxLen)){
    				maxLen = j - i + 1;
    				begin = i;
    			}
    		}
    	}
    	return s.substr(begin,maxLen);
    }
};

方法三：中心扩散法

暴力法采用双指针，验证是否是回文串。

除了枚举字符串的左右边界以外，比较容易想到的是枚举可能出现的回文子串的“中心位置”，从中心位置尝试尽可能扩散出去，得到一个回文串。

思路：

遍历每一个索引，以这个索引为中心，利用“回文串”中心对称的特点，往两边扩散，看最多能扩散多远。

枚举“中心位置”时间复杂度为O(N)，从“中心位置”扩散得到“回文子串”的时间复杂度为O(N)，因此时间复杂度可以降到O(N^2)。

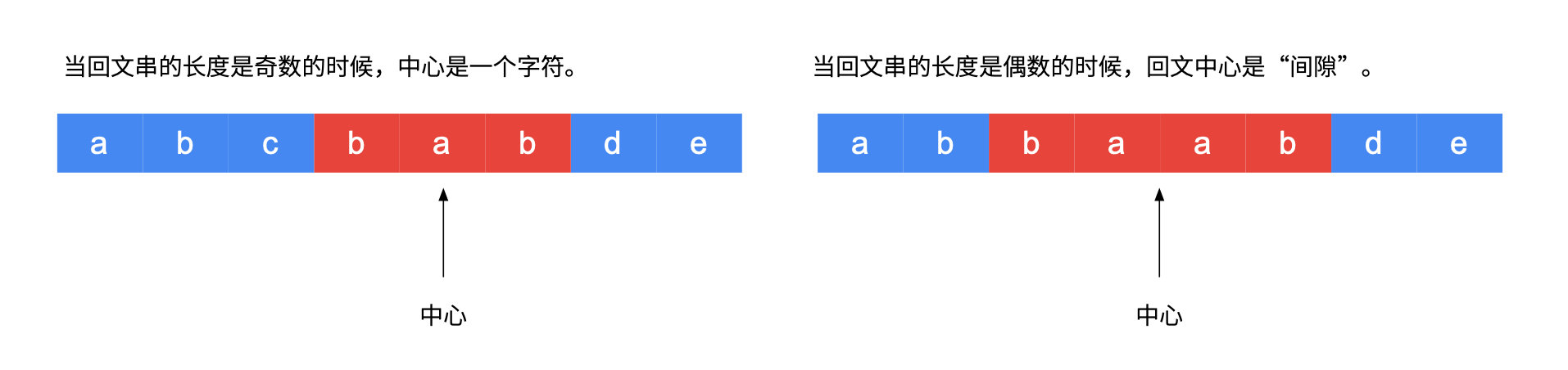
注意：在这里注意一个细节：回文串在长度为奇数和偶数的时候，“回文中心”的形式是不一样的。

  • 奇数回文串的“中心”是一个具体的字符，例如：回文串[^ aba] 的中心是字符[^ b]；
  • 偶数回文串的"中心"是位于中间的两个字符的“空隙”，例如：回文串[^ abba]的中心是两个[^ b]中间的那个“空隙”。

我们可以设计一个方法，兼容以上两种情况：

1、如果传入重合的索引编码，进行中心扩散，此时得到的回文子串的长度是奇数；

2、如果传入相邻的索引编码，进行中心扩散，此时得到的回文子串的长度是偶数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include <string>
#include <vector>

using namespace std;

class Solution {

private:

    string centerSpread(string s, int left, int right) {
        // left = right 的时候，此时回文中心是一个空隙，向两边扩散得到的回文子串的长度是奇数
        // right = left + 1 的时候，此时回文中心是一个字符，向两边扩散得到的回文子串的长度是偶数
        int size = s.size();
        int i = left;
        int j = right;
        while (i >= 0 && j < size) {
            if (s[i] == s[j]) {
                i--;
                j++;
            } else {
                break;
            }
        }
        // 这里要小心，跳出 while 循环时，恰好满足 s.charAt(i) != s.charAt(j)，因此不能取 i，不能取 j
        return s.substr(i + 1, j - i - 1);
    }

public:


    string longestPalindrome(string s) {
        // 特判
        int size = s.size();
        if (size < 2) {
            return s;
        }

        int maxLen = 1;
        string res = s.substr(0, 1);

        // 中心位置枚举到 len - 2 即可
        for (int i = 0; i < size - 1; i++) {
            string oddStr = centerSpread(s, i, i);
            string evenStr = centerSpread(s, i, i + 1);
            string maxLenStr = oddStr.size() > evenStr.size() ? oddStr : evenStr;
            if (maxLenStr.length() > maxLen) {
                maxLen = maxLenStr.size();
                res = maxLenStr;
            }
        }
        return res;
    }
};