CSAPP 第二章 信息的表示和处理

发表于 分类于 ， 阅读次数： Waline： 本文字数： 2.6k 阅读时长 ≈ 2 分钟

信息的表示与处理

2.1 信息存储

大多数计算机使用8位的块，或者字节，作为最小的可寻址的内存单位，而不是访问内存中单独的位。

2.1.1 十六进制表示法

十进制 x 转化为十六进制，可以反复用 16 除 x，得到一个商 q 和一个余数 r，也就是 x = q * 16 + r

反过来也一样，比如我们给定数字 0X7AF,十进制就为

\(7 * 16^2 + 10 * 16 + 15 = 1967\)

2.1.2 字数据大小

每台计算机都有一个字长，指明指针数据的标称大小。因为虚拟地址是以这样一个字来编码的，所以字长决定了虚拟地址空间的最大大小。也就是说，对于一个字长为w的机器，虚拟地址的范围为0~2^w - 1，程序最多访问\(2^w\)个字节。

2.1.3 寻址和字节顺序

  • 小端法： 从最低有效字节到最高有效字节到顺序存储
  • 大端法： 从最高有效字节到最低有效字节的顺序存储

例如：

40004d3: 01 05 43 0b 20 00 add %0x200b43(%rip)

如果我们取出最后4个字节，43 0b 20 00,并且按照相反的顺序写出，得到 00 20 0b 43 去掉开头的0,得到值 0x200b43，这就是右端的数值，所以可以判断是小端法机器。

2.1.4 表示字符串

C语言中字符串被编码为一个以null（其值为0）字符结尾的字符数组，每个字符由ASCII码来表示。例如"12345",结果为31 32 33 34 35 00。

2.1.5 表示代码

程序仅仅只是字节序列。

2.1.6 布尔代数

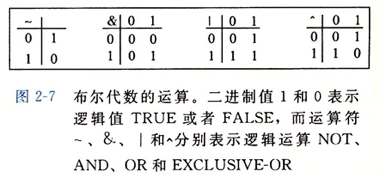
^表示异或，相同为0，不同为1。

(a ^ b) ^ a = b

2.1.7 C语言中的位级运算

|:或

&:与

~: 取反

^: 异或

2.1.8 C语言中的逻辑运算

||: OR

&&: AND

!: NOT

1表示true,0表示false

2.1.9 C语言中的移位运算

逻辑右移和算数右移

x >> k

逻辑右移：在左端补 K 个 0

算数右移：在左端补 K 个最高有效位的值

如果移动的k很大，假设我们的 int为 w = 32

1
2
3
int lval = 0xFEDCBA98 << 32;
int aval = 0xFEDCBA98 >> 36;
unsigned uval = 0xFEDCBA98 >> 40;

在许多机器上，当移动一个w位的值时，移位指令只考虑位移量的低\(log_2w\)位，因此实际上位移量就是通过计算k mod w得到的。

对于无符号数，右移必须是逻辑的。

则上面的就相当于

1
2
3
lval = 0xFEDCBA98 << 0 = 0xFEDCBA98
aval = 0xFEDCBA98 >> 4 = 0xFFEDCBA9
uval = 0xFEDCBA98 >> 8 = 0x00FEDCBA

在C语言中，加减法的优先级比移位运算要高。

2.2 整数表示

2.2.1 整形数据类型

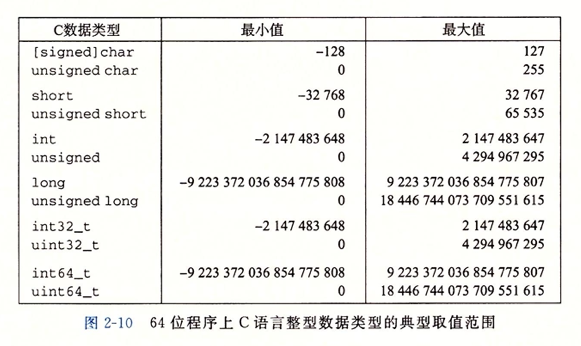
由上面我们可以看出，负数的范围比正数的范围大1

2.2.2 无符号数的编码

假设有一个整数数据类型有w位，我们用一个函数\(B2U_w\) (Binary to Unsigned的缩写，长度为 w )来表示。

无符号数的二进制表示有一个很重要的属性，也就是每个介于\[0-2^w - 1\]之间的数都有唯一一个w位的值编码。

2.2.3 补码编码

表示负数值，最常用的有符号数的计算机表示方式就是补码，将最高有效位解释为负权。

最高位为1，表示负数，为0表示非负数。

补码编码具有唯一性。

2.2.4 有符号数和无符号数之间的转换

对于大多数C语言的实现，处理同样字长的有符号数和无符号数之间相互转换的一般规则是：数值可能会改变，但是位模式不变。

2.2.5 C语言中的有符号数与无符号数

2.2.6 扩展一个数字的位表示

零扩展：要求一个无符号数转换为一个更大的数据类型时，我们只需要在表示的开头添加0

要求一个补码数字转换为一个更大的数据类型，可以执行一个符号扩展，在表示中添加最高有效位的值。

2.3 整数运算

2.4 浮点数

2.4.1 二进制小数

\[ b = \sum_{i = -n}^{m} 2^i * b_i \]

例如 \(101.11_2\) 表示数字 \[ 1 * 2 ^2 + 0 * 2 ^ 1 + 1 * 2 ^ 0 + 1 * 2^{-1} + 1 * 2^{-2} = 4 + 0 + 1 + \frac{1}{2} + \frac{1}{4} = 5\frac{3}{4} \] 小数的二进制表示法只能表示那些能够被写成 \(x * 2^y\) 的数。其他的数只能被近似表示。

2.4.2 IEEE浮点表示

前面提到的定点表示法不能很有效地表示非常大的数。

IEEE 浮点标准用 \(V = (-1)^s * M * 2^E\) 的形式表示一个数。

  • 符号：s决定这个数是负数(s = 1)还是正数(s = 0)
  • 尾数：M 是一个二进制小数
  • 阶码：E 的作用是对浮点数加权，这个权重是2的E次幂。

将浮点数的位表示划分为三个字段。

  • 一个单独的符号位s直接编码符号
  • k位的阶码字段编码E
  • n位小数字段编码尾数M

在单精度浮点格式中，s = 1, k = 8, n = 23

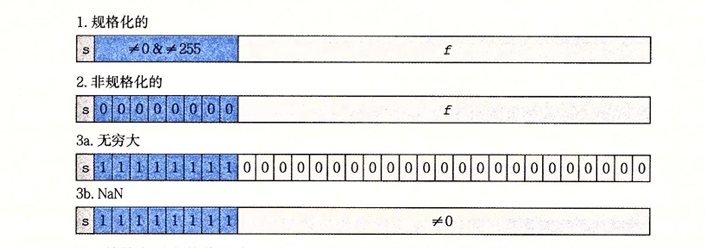
情况一：规格化的值

阶码的值：E = e - Bias其中e是无符号数，其位表示为 \(e_{k-1}...e_1e_0\) ,而 Bias 是一个等于 \(2 ^{k - 1} - 1\) ，（单精度是 127，双精度为 1023）的偏置值。

小数字段 frac 被解释为描述小数值 f ,总是隐含的以 1 开头，尾数定义为 M = 1 + f

情况二：非规格化的值

当阶码为全0时，所表示的数是非规格化形式。阶码值是 E = 1 - Bias,尾数值为M = f，不包含隐含的开头的1。

非规格化数有两个用途：

  1. 提供了一种表示数值 0 的方法
  2. 表示那些非常接近 0.0 的数，它们提供了一种属性，称为逐渐溢出 。其中，可能的数值分布均匀地接近于 0.0

情况三：特殊值

当阶码全为 0 时

当小数域全为0，得到的值表示无穷，当s = 0时是+∞，或者当s = 1时是-∞。

当小数域为非零时，结果值就称为"NaN",即“不是一个数”的缩写。

2.4.4 舍入

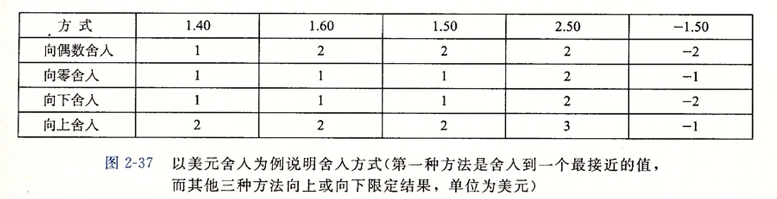
向偶数舍入是在50%的时间里，它将向上舍入，50%的时间向下舍入，就避免了向下舍入时最后平均值偏小和向上舍入时平均值偏大的问题。

2.4.5 浮点运算

浮点加法不具有结合性。