BFS算法解题套路

BFS相对DFS的最主要的区别是：BFS找到的路径一定是最短的，但代价就是空间复杂度可能比DFS大很多。我们后面可以看出来，这里先介绍下BFS框架。

算法框架

BFS的本质就是让你在一副「图」中找到从起点start 到终点rarget的最近距离。

//计算从起点 start 到终点 target 的最近距离
int BFS(Node* start, Node* target){
  queue<Node*> q;
  set<Node*> visited; //避免走回头路
  
  q.push(start);//将起点加入队列
  visited.push(start);
  int step = 0; //记录扩散的步数
  
  while(!q.empty()){
    int sz = q.size();
    /*将当前队列中的所有节点向四周扩散*/
    for(int i = 0; i < sz; i++){
      Node* cur = q.top();
      q.pop();
      /*重点：这里判断是否达到终点*/
      if(cur is target)
        return step;
      /*将 cur 的相邻节点加入队列*/
      for(Node x : cur.adj()){
        if(x not in visited){
          q.push(x);
          visited.push(x);
        }
      }
    }
    //重点：更新步数在这里
    step++;
  }
}

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例：

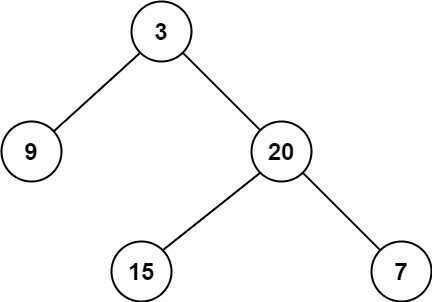
输入：root = [3,9,20,null,null,15,7]

输出：2

思路：

我们首先需要明确一下起点 start 和终点 target 是什么，怎么判断是否到达了终点？

显然起点就是根节点，终点就是最靠近根节点的那个叶子节点。

if(cur->left == nullptr && cur->right == nullptr)
	//达到叶子节点

完整代码如下：

class Solution {
public:
    int minDepth(TreeNode* root) {
        //bfs
        if(root == nullptr) return 0;

        queue<TreeNode*> q;
        q.push(root);
        //root 本身为一层
        int depth = 1;

        while(!q.empty()){
            int sz = q.size();

            for(int i = 0; i < sz; i++){
                TreeNode* cur = q.front();
                q.pop();

                //判断是否达到叶子节点
                if(cur->left == nullptr && cur->right == nullptr){
                    return depth;
                }
                if(cur->left != nullptr){
                    q.push(cur->left);
                }
                if(cur->right != nullptr){
                    q.push(cur->right);
                }
            }
            depth++;
        }
        return depth;
    }
};

这里我们解答下两个问题：

1，为什么BFS可以找到最短路径，DFS不行吗？

首先，BFS的depth每增加一次，队列中的所有节点都向前迈一步，这保证了第一次到达终点的时候，走的步数是最短的。

而DFS当然也可以找到最短路径，但是复杂度相对高很多。因为DFS需要把二叉树所有的分支都搜索完才能对比出最短的路径。

2，既然BFS那么好，为啥还需要DFS

BFS可以找到最短路径，但是空间复杂度高，而DFS的空间复杂度较低。

例如，给你一颗满二叉树，节点数为N，对于DFS来说最坏情况下顶多就是树的高度，也就是O(logN)

而BFS，最坏情况下空间复杂度应该是树的最底层节点的数量，也就是N/2，O(N)

由此可以看出，BFS还是有代价的，一般来说在找最短路径的时候使用BFS，其他时候还是DFS使用比较多一点。