鸡蛋掉落

887. 鸡蛋掉落

给你k枚相同的鸡蛋，并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。

已知存在楼层 f ，满足0 <= f <= n ，任何从 高于 f 的楼层落下的鸡蛋都会碎，从 f 楼层或比它低的楼层落下的鸡蛋都不会破。

每次操作，你可以取一枚没有碎的鸡蛋并把它从任一楼层 x 扔下（满足 1 <= x <= n）。如果鸡蛋碎了，你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎，则可以在之后的操作中 重复使用 这枚鸡蛋。

请你计算并返回要确定f确切的值 的最小操作次数 是多少？

示例：

输入：k = 1, n = 2
输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，肯定能得出 f = 0 。
否则，鸡蛋从 2 楼掉落。如果它碎了，肯定能得出 f = 1 。
如果它没碎，那么肯定能得出 f = 2 。
因此，在最坏的情况下我们需要移动 2 次以确定 f 是多少。

思路：

题目分析：

读完题目之后，也就是让我们找到摔不碎鸡蛋的最高楼层f

假如我们现在不管鸡蛋个数的限制，有7层楼，怎么去找鸡蛋恰好摔碎的那层楼？

最直接的就是线性扫描：先在1楼扔一下，没碎，再去2楼扔一下，没碎，再去3楼......

根据这种策略，最坏情况应该就是找到第7层楼(F = 7)。

既然是至少需要扔几次，那么我们能不能使用二分查找思想

• 先去(1 + 7) / 2 = 4楼扔一下，如果碎了，说明f < 4，我就去第(1 + 3) / 2 = 2层
• 如果没碎，说明f > 4，我就去第(5 + 7) / 2 = 6层去试......

这种情况下，最坏情况应该是试到第 7 层鸡蛋还没碎(f = 7)，或者一直碎到第 1 层(f = 1)。然而无论哪种最坏情况，只需要试log7，向上取整，也就是 3 次，比之前尝试 7 次要少。

实际上，如果不限制鸡蛋个数的话，二分思想显然可以得到最少尝试次数，但现在给了鸡蛋个数的限制k，直接使用二分思想就不可以了。

ps: 后面会给出二分思路

思路分析：

对于动态规划问题，我们只需要明白框架：即这个问题有什么「状态」，有什么「选择」，然后穷举。

「状态」很明显，就是当前拥有的鸡蛋数k和需要测试的楼层数n。

「选择」其实就是去选择哪层楼扔鸡蛋。

那么动态规划的基本思想就形成了：肯定是个二维的dp数组或者带有两个状态的dp函数来表示状态转移；外加一个for循环来遍历所有选择，选择最优的选择更新状态：

//当前状态为 k 个鸡蛋，面对 n 层楼
//返回这个状态下的最优结果
int dp(k, n):
	int res;
	for(1 <= i <= n)
		res = min(res, 这次在第 i 层楼扔鸡蛋)
	return res;

我们选择在第i层楼扔了鸡蛋之后，可能出现两种情况：鸡蛋碎了，鸡蛋没碎。这就是状态转移。

如果鸡蛋碎了，那么鸡蛋的个数k应该减一，搜索的楼层区间从[1...n]变为[1...i - 1]，共i-1层楼；

如果鸡蛋没碎，那么鸡蛋个数k不变，搜索的楼层区间应该从[1...n]变为[i+1...n]共n-i层楼；

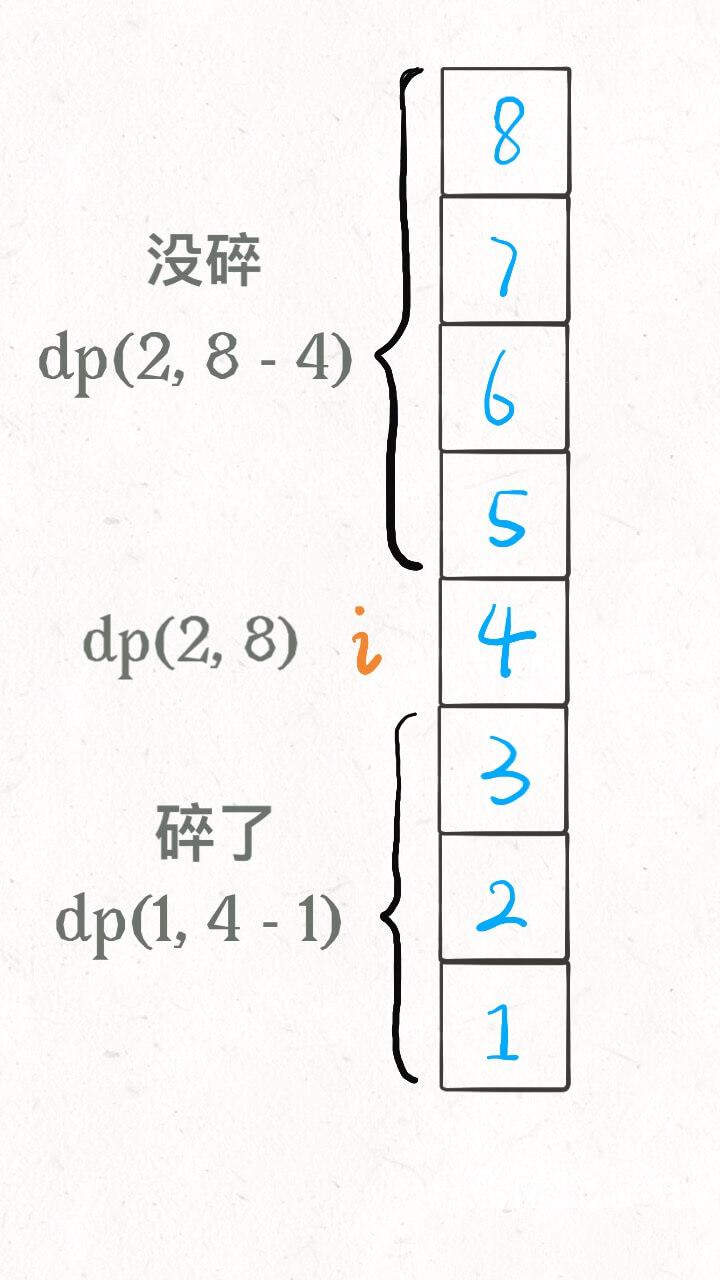
递归的base case也很容易理解：当楼层数n ==0时，显然不需要扔鸡蛋；当鸡蛋数k为 1 时，显然只能线性扫描所有楼层：

class Solution {
public:
    int superEggDrop(int k, int n) {
        return dp(k, n);
    }
    int dp(int k, int n){
        //base case
        if(n == 0 || n == 1 || k == 1) return n;

        int res = n;
        for(int i = 1; i <= n; i++){
            //最坏情况下的最少扔鸡蛋个数 碎了  没碎
            res = min(res, max(dp(k, n - i), dp(k - 1, i - 1)) + 1);
        }
        return res;
    }
};

很明显存在重复子问题，使用备忘录优化：

class Solution {
public:
    vector<vector<int> > memo;
    int superEggDrop(int k, int n) {
        memo.resize(k + 1, vector<int>(n + 1, -1));
        return dp(k, n);
    }
    int dp(int k, int n){
        // base case
        //如果只剩一个鸡蛋，线性遍历
        if(k == 1 || n == 0 || n == 1) return n;

        //避免重复计算
        if(memo[k][n] != -1){
            return memo[k][n];
        }

        int res = n;
        //穷举所有可能的选择
        for(int i = 1; i <= n; i++){
            //最坏情况下的最少扔鸡蛋个数
            res = min(res, max(dp(k, n - i), dp(k - 1, i - 1)) + 1);
        }
        //记入备忘录
        memo[k][n] = res;
        return res;
    }
};

动态规划算法时间复杂度就是子问题个数 X 函数本身的复杂度。

for循环复杂度为O(N),子问题个数就是不同状态组合的总数，显然是两个状态的乘积，也就是O(KN)。

所以总的时间复杂度为O(KN^2)，空间复杂度为O(KN)。

二分搜索优化

我们先回忆下前面算法的思路：

1、暴力穷举尝试在所有楼层 1 <= i <= N 扔鸡蛋，每次选择尝试次数最少的那一层；

2、每次扔鸡蛋有两种可能，要么碎，要么没碎；

3、如果鸡蛋碎了，F 应该在第 i 层下面，否则，F 应该在第 i 层上面；

4、鸡蛋是碎了还是没碎，取决于哪种情况下尝试次数更多，因为我们想求的是最坏情况下的结果。

状态转移方程为：

​ \(dp(k,n) = min(max(dp(k - 1, i - 1), dp(k, n - i)) + 1)\)

我们二分查找优化的思路思路就是根据这个状态转移方程来的，所以需要我们理解这个状态转移。

首先我们根据dp(k,n)数组的定义：有 k 个鸡蛋面对 n 层楼，最少需要扔几次，很容易知道 k 固定时，这个函数会随着 n 的增加一定是单增的。因为随着楼层的增加，测试次数也一定会增加。

那么注意dp(k-1, i-1)和dp(k, n-i)这两个函数，其中 i 是从 1 到 N 单增的，如果我们固定 K 和 N，把这两个函数看做关于 i 的函数，前者随着 i 的增加应该也是单调递增的，而后者随着 i 的增加应该是单调递减的：

这时候求二者的较大值，再求这些最大值之中的最小值，其实就是求这两条直线交点，也就是红色折线的最低点嘛。

class Solution {
public:
    vector<vector<int> > memo;
    int superEggDrop(int k, int n) {
        memo.resize(k + 1, vector<int>(n + 1, -1));
        return dp(k, n);
    }
    int dp(int k, int n){
        //base case
        if(k == 1 || n == 0 || n == 1) return n;

        //避免重复计算
        if(memo[k][n] != -1){
            return memo[k][n];
        }

        int res = n * n;
        //用二分搜索替代线性搜索
        int lo = 1, hi = n;
        while(lo <= hi){
            int mid = (lo + hi) / 2;
            //碎了
            int broken = dp(k - 1, mid - 1);
            //没碎
            int no_broken = dp(k, n - mid);

            //res = min(max(碎，没碎) + 1)
            if(broken > no_broken){
                //碎了
                hi = mid - 1;
                res = min(res, broken + 1);
            }else{
                //没碎
                lo = mid + 1;
                res = min(res, no_broken + 1);
            }
        }
        memo[k][n] = res;
        return res;
    }
};

因为用了二分搜索，所以复杂度为O(logn)，子问题个数为O(kn)

所以总的时间复杂度为O(knlogn)。

重新定义状态转移

dp[k][m] = n 表示当前有 k 个鸡蛋， 可以尝试扔 m 次鸡蛋，在这个状态下，最坏情况下最多能确定一栋 n 层的

1、无论你在哪层楼扔鸡蛋，鸡蛋只可能摔碎或者没摔碎，碎了的话就测楼下，没碎的话就测楼上。

2、无论你上楼还是下楼，总的楼层数 = 楼上的楼层数 + 楼下的楼层数 + 1（当前这层楼）。

转移方程：

dp[k][m] = dp[k][m-1] + dp[k - 1][m - 1] + 1;

时间复杂度为O(kn)

class Solution {
public:
    int superEggDrop(int k, int n) {
        vector<vector<int> > dp(k + 1, vector<int>(n + 1, 0));

        int m = 0;
        while(dp[k][m] < n){
            m++;
            for(int i = 1; i <= k; i++){
                dp[i][m] = dp[i][m - 1] + dp[i - 1][m - 1] + 1;
            }
        }
        return m;
    }
};