盛水问题

发表于 分类于 ， 阅读次数： Waline： 本文字数： 3.7k 阅读时长 ≈ 3 分钟

11. 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例：

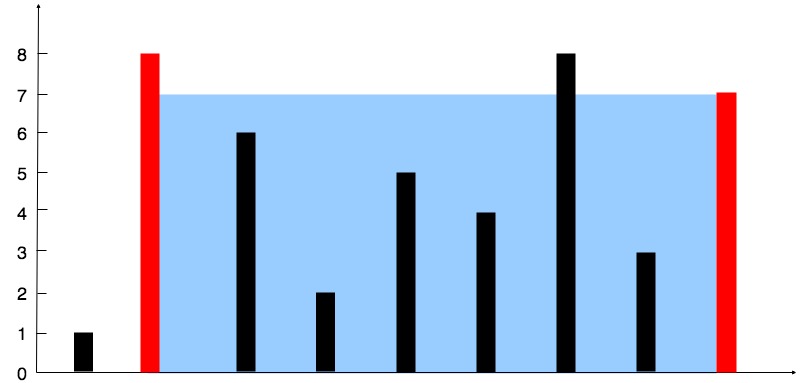
输入：[1,8,6,2,5,4,8,3,7]

输出：49

解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

思路：

我们使用双指针来解决。

left和right两个指针从两端向中心收缩，一边收缩一边计算[left,right]之间的矩阵面积，取最大的面积即是答案。

现在关键是要向那边收缩？

我们知道，矩形的高度是由最短的边决定的。所以移动较低的那条边，矩阵的高度可能会变高。

min(height[left],height[right])。如果移动高度较高的边，则矩阵的高度不可能变高。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0, right = height.size() - 1;
        int res = 0;
        while(left < right){
            int cur_ares = min(height[left], height[right]) * (right - left);
            res = max(res, cur_ares);
            //移动到较低的一边
            if(height[left] < height[right]){
                left++;
            }else{
                right--;
            }
        }
        return res;
    }
};

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例：

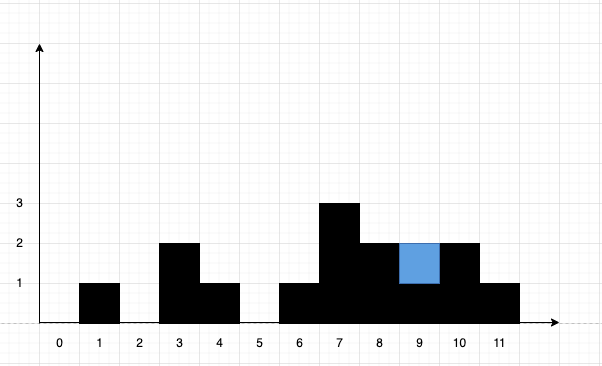
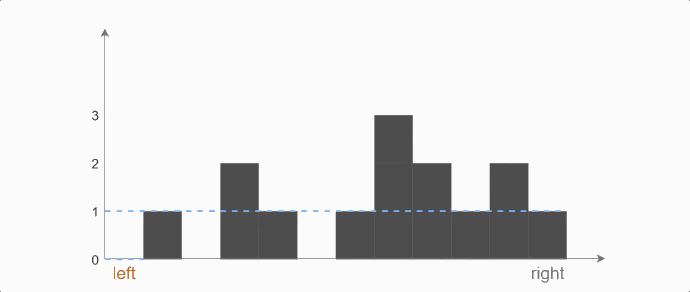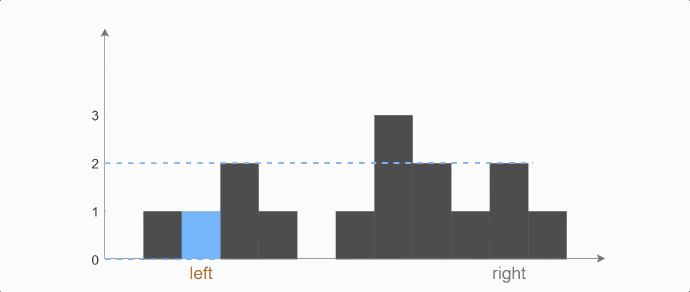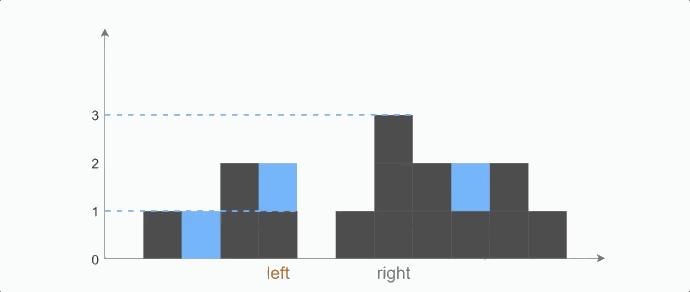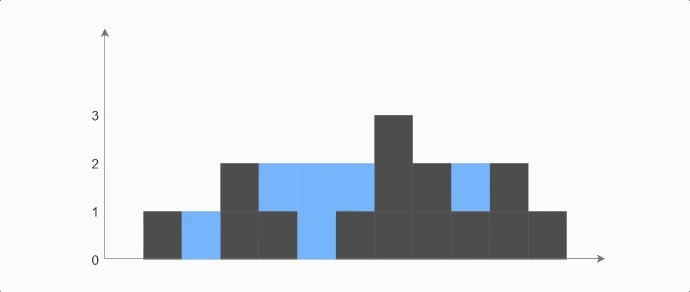
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]

输出：6

解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

思路：

方法一：单调栈

具体的思想可以看单调栈

我们把下标入栈，分别淹没现在所在的这一行元素中可以淹没的。

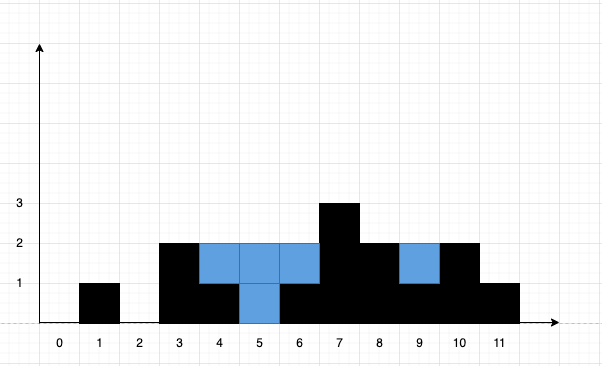
我们只需要判断此时矩阵中需要填的水，累加就是答案，矩阵的高是由左边界和右边界的最小值决定的，我们需要注意的是，我们是每次处理一层，所以要把左边界和右边界中的最小值减去要弹出的元素的高度。

1
2
3
4
5
6
int top = s.top();
s.pop();
int left = i;
int curryWidth = s.top() - left - i;
int currHeight = min(height[left], height[s.top()]) - height[top]
ans += currWidth * currHeight;

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> s;
        int ans = 0;
        //倒着进栈
        for(int i = height.size() - 1; i >= 0; i--){
            //判断个子高低
            int temp = height[i];
            while(!s.empty() && temp >= height[s.top()]){
                int top = s.top();
                s.pop();
                if(s.empty()){
                    break;
                }
                int left = i;
                int currWidth = s.top() - left - 1;
                int currHeight = min(height[left], height[s.top()]) - height[top];
                ans += currWidth * currHeight;
            }
            s.push(i);
        }
        return ans;
    }
};

时间复杂度和空间复杂度都为O(N)

方法二：双指针

我们先明确几个变量的意思：

left_max：左边的最大值，它是从左往右遍历找到的

right_max：右边的最大值，它是从右往左遍历找到的

left：从左往右处理的当前下标

right：从右往左处理的当前下标

定理一：在某个位置i处，它能存的水，取决于它左右两边的最大值中较小的一个。

定理二：当我们从左往右处理到left下标时，左边的最大值left_max对它而言是可信的，但right_max对它而言是不可信的。（见下图，由于中间状况未知，对于left下标而言，right_max未必就是它右边最大的值）

定理三：当我们从右往左处理到right下标时，右边的最大值right_max对它而言是可信的，但left_max对它而言是不可信的。

1
2
3
4
5
6
                                   right_max
 left_max                             __
   __                                |  |
  |  |__   __??????????????????????  |  |
__|     |__|                       __|  |__
        left                      right

对于位置left而言，它左边最大值一定是left_max，右边最大值“大于等于”right_max，这时候，如果left_max<right_max成立，那么它就知道自己能存多少水了。无论右边将来会不会出现更大的right_max，都不影响这个结果。 所以当left_max<right_max时，我们就希望去处理left下标，反之，我们希望去处理right下标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int trap(vector<int>& height) {
        int res = 0;
        int left = 0, right = height.size() - 1;
        int leftMax = 0, rightMax = 0;
        while(left < right){
            leftMax = max(leftMax, height[left]);
            rightMax = max(rightMax, height[right]);
            if(height[left] < height[right]){
                res += leftMax - height[left];
                ++left;
            }else{
                res += rightMax - height[right];
                --right;
            }
        }
        return res;
    }
};

时间复杂度为O(N)空间复杂度为O(1)。