滑动窗口

发表于 分类于 ， 阅读次数： Waline： 本文字数： 12k 阅读时长 ≈ 11 分钟

对于子串问题，大部分都可以通过滑动窗口来解决。说起来滑动窗口的思路非常简单，就是维护一个窗口，不断滑动，然后更新答案。这个算法的时间复杂度为O(N)，比字符串暴力算法要高效多了，这里我们可以学习下labuladong大神的框架。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;
    
    int left = 0, right = 0;
    int valid = 0; 
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移（增大）窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/
        
        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移（缩小）窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

通过下面的一道题来深入了解下滑动窗口：

76. 最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。 如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例：

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"

思路：

第一步想到的肯定是暴力算法，就是在s中找到包含T中全部字母的一个子串，且这个子串一定是所有可能子串中最短的。

1
2
3
4
for(int i = 0; i < s.size(); i++)
	for(int j = i + 1; j < s.size(); j++)
		if(s[i:j]) 包含 t 中的所有字母:
			更新答案

思路非常简单，算法时间复杂度肯定大于O(N^2)。

滑动窗口算法的思路是这样的：

1，我们在字符串s中使用双指针中的左右指针技巧，初始化left=right=0，把索引左闭右开区间[left, right]称为一个「窗口」。

PS：理论上你可以设计两端都开或者两端都闭的区间，但设计为左闭右开区间是最方便处理的。因为这样初始化 left = right = 0 时区间 [0, 0) 中没有元素，但只要让 right 向右移动一位，区间 [0, 1) 就包含一个元素 0 了。如果你设置为两端都开的区间，那么让 right 向右移动一位后开区间 (0, 1) 仍然没有元素；如果你设置为两端都闭的区间，那么初始区间 [0, 0] 就包含了一个元素。这两种情况都会给边界处理带来不必要的麻烦。

2，我们先不断地增加 right 指针扩大窗口 [left, right)，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。

3，此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right)，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果。

4，重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。

下面画图理解一下，needs 和 window 相当于计数器，分别记录 T 中字符出现次数和「窗口」中的相应字符的出现次数。

初始状态：

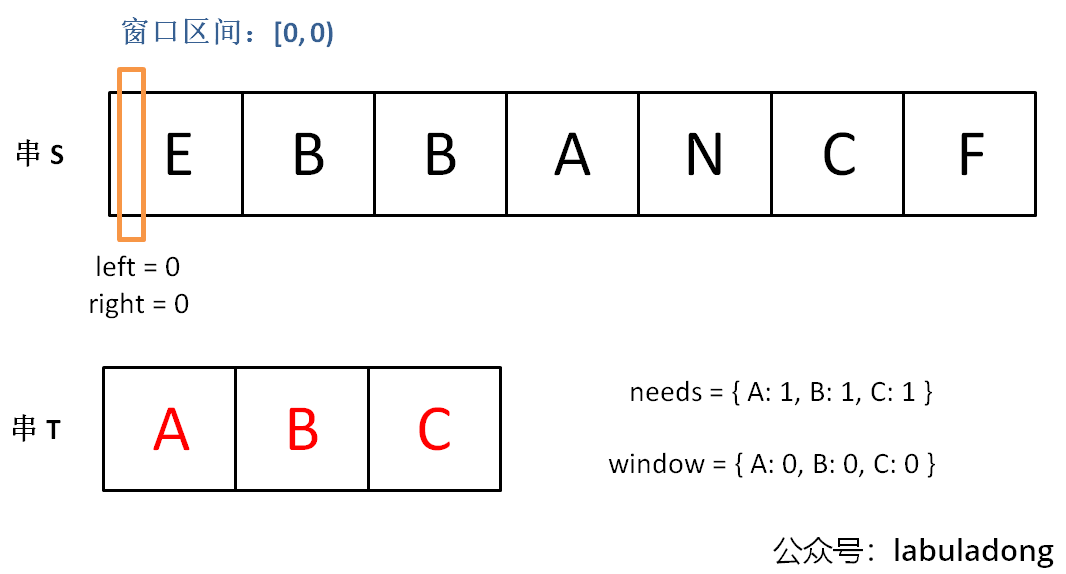
增加 right，直到窗口 [left, right] 包含了 T 中所有字符：

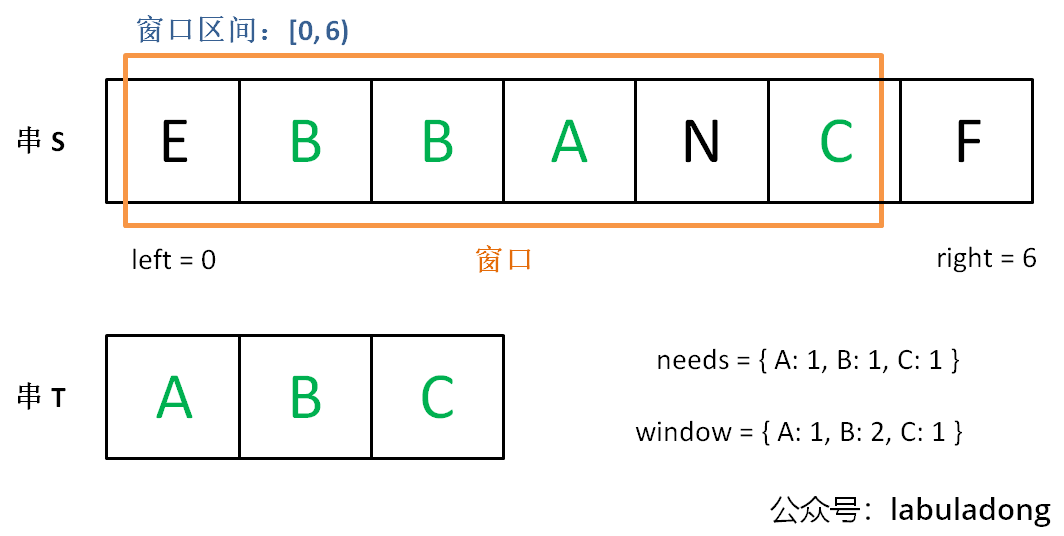
现在开始增加 left，缩小窗口 [left, right]：

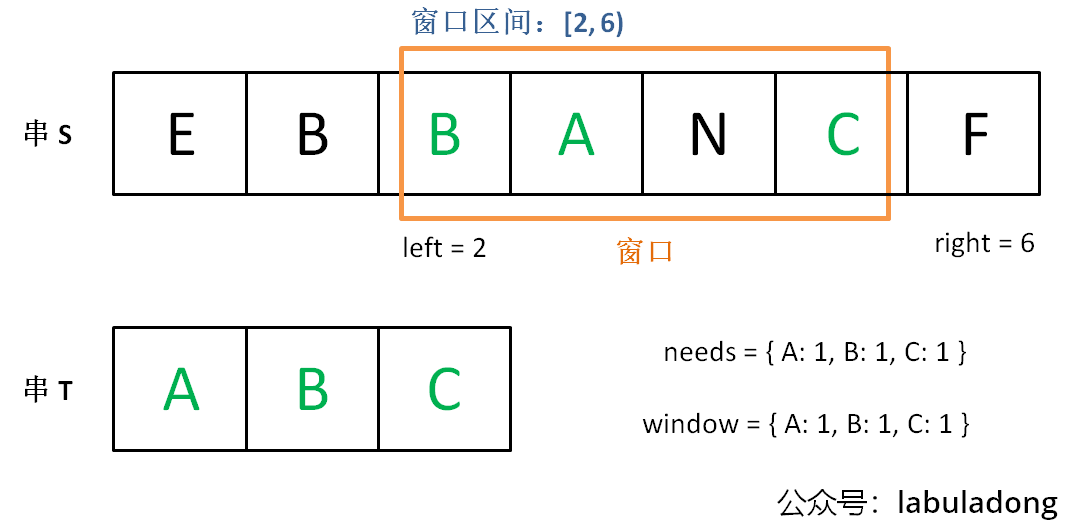
直到窗口中的字符串不再符合要求，left 不再继续移动：

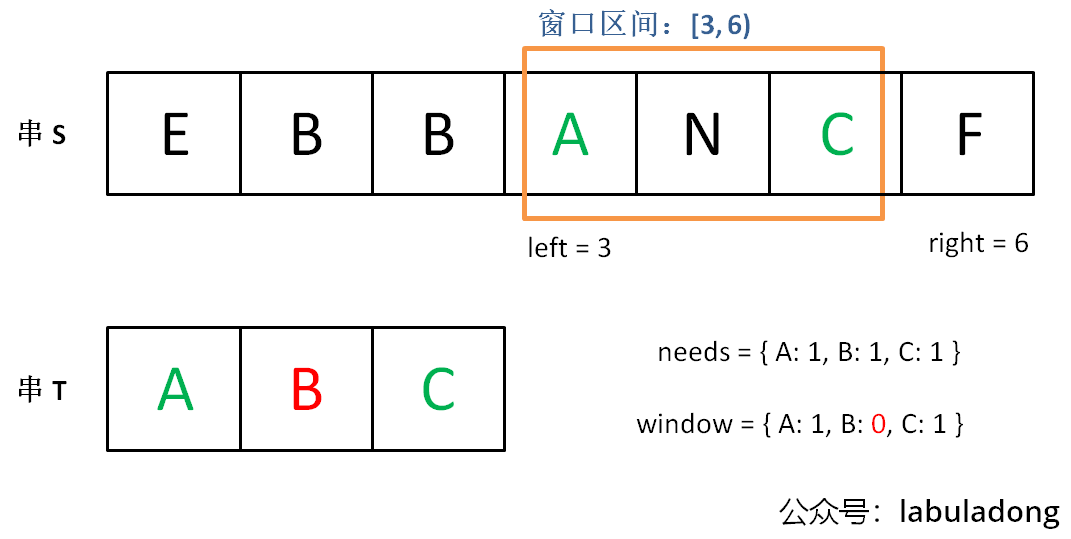
之后重复上述过程，先移动 right，再移动 left…… 直到 right 指针到达字符串 S 的末端，算法结束。

如果你能够理解上述过程，恭喜，你已经完全掌握了滑动窗口算法思想。现在我们来看看这个滑动窗口代码框架怎么用：

首先，初始化 window 和 need 两个哈希表，记录窗口中的字符和需要凑齐的字符：

1
2
unordered_map<char, int> need, window;
for (char c : t) need[c]++;

然后，使用 left 和 right 变量初始化窗口的两端，不要忘了，区间 [left, right) 是左闭右开的，所以初始情况下窗口没有包含任何元素：

1
2
3
4
5
int left = 0, right = 0;
int valid = 0; 
while (right < s.size()) {
    // 开始滑动
}

其中 valid 变量表示窗口中满足 need 条件的字符个数，如果 valid 和 need.size 的大小相同，则说明窗口已满足条件，已经完全覆盖了串 T。

1、当移动 right 扩大窗口，即加入字符时，应该更新哪些数据？

2、什么条件下，窗口应该暂停扩大，开始移动 left 缩小窗口？

3、当移动 left 缩小窗口，即移出字符时，应该更新哪些数据？

4、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？

如果一个字符进入窗口，应该增加 window 计数器；如果一个字符将移出窗口的时候，应该减少 window 计数器；当 valid 满足 need 时应该收缩窗口；应该在收缩窗口的时候更新最终结果。

下面是完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
#include <limits>
using namespace std;

class Solution {
public:
    string minWindow(string s, string t) {
        unordered_map<char, int> need, window;
        for(char c : t) need[c]++;

        int left = 0, right = 0;
        // 使用 valid 来计算符合 t 的元素数量
        int valid = 0;
        //记录最小覆盖子串的起始索引及长度
        int start = 0, len = INT_MAX;
        while(right < s.size()){
            // c 是将移入窗口的字符
            char c = s[right];
            // 右移窗口
            right++;
            // 进行窗口内数据的一系列更新
            if(need.count(c)){
                window[c]++;
                // 当前元素符合所需要的个数
                if(window[c] == need[c]){
                    valid++;
                }
            }

            // 判断左侧窗口是否要收缩
            // 元素已经可以在 s 中找到
            while(valid == need.size()){
                //在这里更新最小覆盖子串
                if(right - left < len){
                    start = left;
                    // 记录子串的长度
                    len = right - left;
                }

                // d 是将移出窗口的字符
                char d = s[left];
                // 左移窗口
                left++;
                // 进行窗口内数据的一系列更新
                if(need.count(d)){
                    if(window[d] == need[d])
                        valid--;
                    window[d]--;
                }
            }
        }
        // 返回最小覆盖子串
        return len == INT_MAX ? "" : s.substr(start, len);
    }
};

需要注意的是，当我们发现某个字符在 window 的数量满足了 need 的需要，就要更新 valid，表示有一个字符已经满足要求。而且，你能发现，两次对窗口内数据的更新操作是完全对称的。

当 valid == need.size() 时，说明 T 中所有字符已经被覆盖，已经得到一个可行的覆盖子串，现在应该开始收缩窗口了，以便得到「最小覆盖子串」。

移动 left 收缩窗口时，窗口内的字符都是可行解，所以应该在收缩窗口的阶段进行最小覆盖子串的更新，以便从可行解中找到长度最短的最终结果。

567. 字符串的排列

给你两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的排列。如果是，返回 true ；否则，返回 false 。

换句话说，s1 的排列之一是 s2 的 子串 。

示例：

输入：s1 = "ab" s2 = "eidbaooo"
输出：true
解释：s2 包含 s1 的排列之一 ("ba").

思路：

这种题目，是明显的滑动窗口算法，相当给你一个 S 和一个 T，请问你 S 中是否存在一个子串，包含 T 中所有字符且不包含其他字符？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
public:
    bool checkInclusion(string s1, string s2) {
        unordered_map<char, int> need, window;
        //统计元素和个数
        for(char c : s1) need[c]++;
        
        int left = 0, right = 0;
        int valid = 0;

        while(right < s2.size()){
            // c 是将要移入窗口的字符
            char c = s2[right];
            // 右移窗口
            right++;
            //进行窗口内数据的更新
            if(need.count(c)){
                window[c]++;
                if(need[c] == window[c]){
                    valid++;
                }
            }

            //判断左侧窗口是否要收缩
            while(right - left >= s1.size()){
                // 在这里更新子串
                if(valid == need.size())
                    return true;

                // d 是将要移出窗口的字符
                char d = s2[left];
                // 左移窗口
                left++;
                // 进行窗口内数据的更新
                if(need.count(d)){
                    if(window[d] == need[d])
                        valid--;
                    window[d]--;
                }
            }
        }
        return false;
    }
};

对于这道题的解法代码，基本上和最小覆盖子串一模一样，只需要改变两个地方：

1、本题移动 left 缩小窗口的时机是窗口大小大于 t.size() 时，应为排列嘛，显然长度应该是一样的。

2、当发现 valid == need.size() 时，就说明窗口中就是一个合法的排列，所以立即返回 true。

至于如何处理窗口的扩大和缩小，和最小覆盖子串完全相同。

HJ63 DNA序列

描述：

一个 DNA 序列由 A/C/G/T 四个字母的排列组合组成。 G 和 C 的比例（定义为 GC-Ratio ）是序列中 G 和 C 两个字母的总的出现次数除以总的字母数目（也就是序列长度）。在基因工程中，这个比例非常重要。因为高的 GC-Ratio 可能是基因的起始点。

给定一个很长的 DNA 序列，以及限定的子串长度 N ，请帮助研究人员在给出的 DNA 序列中从左往右找出 GC-Ratio 最高且长度为 N 的第一个子串。

DNA序列为 ACGT 的子串有: ACG , CG , CGT 等等，但是没有 AGT ， CT 等等

数据范围：字符串长度满足 \(1≤n≤1000\) ，输入的字符串只包含 A/C/G/T 字母

输入描述：

输入一个string型基因序列，和int型子串的长度

输出描述：

找出GC比例最高的子串,如果有多个则输出第一个的子串

示例：

输入：

ACGT
2

输出：

CG

说明：

ACGT长度为2的子串有AC,CG,GT3个，其中AC和GT2个的GC-Ratio都为0.5，CG为1，故输出CG

思路：

也是滑动窗口问题，套用我们之前的框架。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <bits/stdc++.h>
#include <limits>
using namespace std;

/*
滑动窗口
*/

int main(){
    string s;
    int n;
    while(cin >> s >> n){
        int left = 0, right = 0;
        int valid = 0;
        
        int start = 0;
        float res = -1;
        while(right < s.size()){
            // c 是将要移入窗口的字符
            char c = s[right];
            // 右移窗口
            right++;
            // 进行窗口内数据的更新
            if(c == 'C' || c == 'G'){
                valid++;
            }
            
            // 判断左侧窗口是否需要收缩
            while((right - left) == n){
                //更新子串
                float tmp = valid / (n * 1.0);
                if(tmp > res){
                    res = tmp;
                    start = left;
                }
                
                // d 是将移出窗口的字符
                char d = s[left];
                // 左移窗口
                left++;
                //进行窗口内的更新
                if(d == 'C' || d == 'G'){
                    valid--;
                }
            }
        }
        cout << s.substr(start, n) << endl;
    }
    return 0;
}

对于这道题的解法代码，只需要改变两个地方：

1，移动left收缩窗口的时机为当(right - left) > n时，因为给定了子串长度，当长度一样时，就是答案。

2，当发现(right - left) == n时，就说明窗口中就是一个合法的子串，我们取所有合法子串中包含C,G比例最高的，然后记录开始位置，加上给定的子串长度，我们就可以得出答案。

438. 找到字符串中所有字母异位词

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。

示例：

输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。

思路：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        vector<int> res;
        unordered_map<char, int> need, window;
        for(char c : p) need[c]++;

        int left = 0, right = 0;
        int valid = 0;

        while(right < s.size()){
            // c 是将要移入窗口的字符
            char c = s[right];
            // 右移窗口
            right++;
            // 进行窗口内数据的更新
            if(need.count(c)){
                window[c]++;
                if(need[c] == window[c])
                    valid++;
            }

            // 判断左侧窗口是否需要收缩
            while((right - left) == p.size()){
                // 在这里更新子串
                if(valid == need.size()){
                    res.push_back(left);
                }
                // d 是将要移出窗口的字符
                char d = s[left];
                // 左移窗口
                left++;

                // 进行窗口内数据的更新
                if(need.count(d)){
                    if(need[d] == window[d])
                        valid--;
                    window[d]--;
                }
            }
        }
        return res;
    }
};

3. 无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例：

输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

思路：

这道题比之前灵活了不少，需要我们改动下框架，更新窗口内数据也只需要简单的更新计数器window即可。

当 window[c] 值大于 1 时，说明窗口中存在重复字符，不符合条件，就该移动 left 缩小窗口了嘛。

唯一需要注意的是，在哪里更新结果 res 呢？我们要的是最长无重复子串，哪一个阶段可以保证窗口中的字符串是没有重复的呢？

这里和之前不一样，要在收缩窗口完成后更新 res，因为窗口收缩的 while 条件是存在重复元素，换句话说收缩完成后一定保证窗口中没有重复嘛。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
#include <limits>
using namespace std;

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_map<char, int> window;
        int left = 0, right = 0;
        int res = 0;

        while(right < s.size()){
            char c = s[right];
            right++;

            // 进行窗口内数据的更新
            window[c]++;

            // 判断左侧窗口是否需要收缩
            while(window[c] > 1){
                char d = s[left];
                left++;
                // 进行窗口内数据的更新
                window[d]--;
            }
            res = max(res, right - left);
        }
        return res;
    }
};

239. 滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置 最大值

[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7

思路：

1，如果队列不空且当前元素大于队尾元素，则将队尾元素删除，直到队列为空或者当前元素小于新的队尾元素

2，保持队列q当前递减，第一个数就是窗口内的最大值，第二个为第二大......

3，当前首元素的下标小于滑动窗口左侧边界 left 时， 表示队首元素已经不再滑动窗口内，因此将其从队首移除

4，由于数组下标从 0 开始，因此当窗口边界 right + 1 大于等于窗口 k 时， 意味着窗口形成。此时，队首元素就是该窗口的最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <bits/stdc++.h>
#include <limits>
using namespace std;

/*
优化
时机复杂度O(N)
*/
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        if(nums.size() < k || k <= 0) return {};
        deque<int> q;
        vector<int> res(nums.size() - k + 1);

        for(int right = 0; right < nums.size(); right++){
            //如果队列不空且当前元素大于队尾元素，则将队尾元素删除
            //直到队列为空或者当前元素小于新的队尾元素
            while(!q.empty() && nums[right] >= nums[q.back()]){
                q.pop_back();
            }
            //存储元素下标
            q.push_back(right);

            //计算窗口左侧边界
            int left = right - k + 1;
            // 当前首元素的下标小于滑动窗口左侧边界 left 时
            // 表示队首元素已经不再滑动窗口内，因此将其从队首移除
            if(q.front() < left){
                q.pop_front();
            }

            // 由于数组下标从 0 开始，因此当窗口边界 right + 1 大于等于窗口 k 时
            // 意味着窗口形成。此时，队首元素就是该窗口的最大值。
            if(right + 1 >= k){
                res[left] = nums[q.front()];
            }
        }
        return res;
    }
};