正则表达式匹配

发表于 分类于 ， 阅读次数： Waline： 本文字数： 6k 阅读时长 ≈ 5 分钟

这两个通配符是最常用的，其中点号「.」可以匹配任意一个字符，星号「*」可以让之前的那个字符重复任意次数（包括 0 次）。

比如说模式串".a*b"就可以匹配文本"zaaab"，也可以匹配"cb"；模式串"a..b"可以匹配文本"amnb"；而模式串".*"就比较牛逼了，它可以匹配任何文本。

题目会给我们输入两个字符串s和p，s代表文本，p代表模式串，请你判断模式串p是否可以匹配文本s。我们可以假设模式串只包含小写字母和上述两种通配符且一定合法，不会出现*a或者b**这种不合法的模式串，

总结自labuladong大神

10. 正则表达式匹配

给你一个字符串s和一个字符规律p，请你来实现一个支持'.'和 '*' 的正则表达式匹配。

  • '.' 匹配任意单个字符

  • '*' 匹配零个或多个前面的那一个元素

    所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

示例：

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

输入：s = "aa", p = "a*"

输出：true

解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

输入：s = "ab", p = ".*"

输出：true

解释："." 表示可匹配零个或多个（''）任意字符（'.'）。

思路：

我们先脑补一下，s和p相互匹配的过程大致是，两个指针i, j分别在s和p上移动，如果最后两个指针都能移动到字符串的末尾，那么就匹配成功，反之则匹配失败。

正则表达算法问题只需要把住一个基本点：看两个字符是否匹配，一切逻辑围绕匹配/不匹配两种情况展开即可。

如果不考虑*通配符，面对两个待匹配字符s[i]和p[j]，我们唯一能做的就是看他俩是否匹配：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool isMatch(string s, string p) {
    int i = 0, j = 0;
    while (i < s.size() && j < p.size()) {
        // 「.」通配符就是万金油
        if (s[i] == p[j] || p[j] == '.') {
            // 匹配，接着匹配 s[i+1..] 和 p[j+1..]
            i++; j++;
        } else {
            // 不匹配
            return false;
        }
    }
    return i == j;
}

那么考虑一下，如果加入*通配符，局面就会稍微复杂一些，不过只要分情况来分析，也不难理解。

当p[j + 1]为*通配符时，我们分情况讨论下：

1、如果匹配，即s[i] == p[j]，那么有两种情况：

1.1p[j]有可能会匹配多个字符，比如s = "aaa", p = "a*"，那么p[0]会通过*匹配 3 个字符"a"。

1.2p[i]也有可能匹配 0 个字符，比如s = "aa", p = "a*aa"，由于后面的字符可以匹配s，所以p[0]只能匹配 0 次。

2、如果不匹配，即s[i] != p[j]，只有一种情况：

p[j]只能匹配 0 次，然后看下一个字符是否能和s[i]匹配。比如说s = "aa", p = "b*aa"，此时p[0]只能匹配 0 次。

综上，可以把之前的代码针对*通配符进行一下改造：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
if (s[i] == p[j] || p[j] == '.') {
    // 匹配
    if (j < p.size() - 1 && p[j + 1] == '*') {
        // 有 * 通配符，可以匹配 0 次或多次
    } else {
        // 无 * 通配符，老老实实匹配 1 次
        i++; j++;
    }
} else {
    // 不匹配
    if (j < p.size() - 1 && p[j + 1] == '*') {
        // 有 * 通配符，只能匹配 0 次
    } else {
        // 无 * 通配符，匹配无法进行下去了
        return false;
    }
}

整体的思路已经很清晰了，但现在的问题是，遇到*通配符时，到底应该匹配 0 次还是匹配多次？多次是几次？

你看，这就是一个做「选择」的问题，要把所有可能的选择都穷举一遍才能得出结果。动态规划算法的核心就是「状态」和「选择」，「状态」无非就是i和j两个指针的位置，「选择」就是p[j]选择匹配几个字符。

动态规划解法

根据「状态」，我们可以定义一个dp函数：

bool dp(string& s, int i, string& p, int j);

dp函数的定义如下：

若dp(s,i,p,j) = true，则表示s[i..]可以匹配p[j..]；

若dp(s,i,p,j) = false，则表示s[i..]无法匹配p[j..]。

根据这个定义，我们想要的答案就是i = 0,j = 0时dp函数的结果，所以可以这样使用这个dp函数：

1
2
3
bool isMatch(string s, string p) {
    // 指针 i，j 从索引 0 开始移动
    return dp(s, 0, p, 0);

可以根据之前的代码写出dp函数的主要逻辑：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
bool dp(string& s, int i, string& p, int j) {
    if (s[i] == p[j] || p[j] == '.') {
        // 匹配
        if (j < p.size() - 1 && p[j + 1] == '*') {
            // 1.1 通配符匹配 0 次或多次
            return dp(s, i, p, j + 2)
                || dp(s, i + 1, p, j);
        } else {
            // 1.2 常规匹配 1 次
            return dp(s, i + 1, p, j + 1);
        }
    } else {
        // 不匹配
        if (j < p.size() - 1 && p[j + 1] == '*') {
            // 2.1 通配符匹配 0 次
            return dp(s, i, p, j + 2);
        } else {
            // 2.2 无法继续匹配
            return false;
        }
    }
}

1.1 通配符匹配 0 次或多次

将j加 2，i不变，含义就是直接跳过p[j]和之后的通配符，即通配符匹配 0 次：

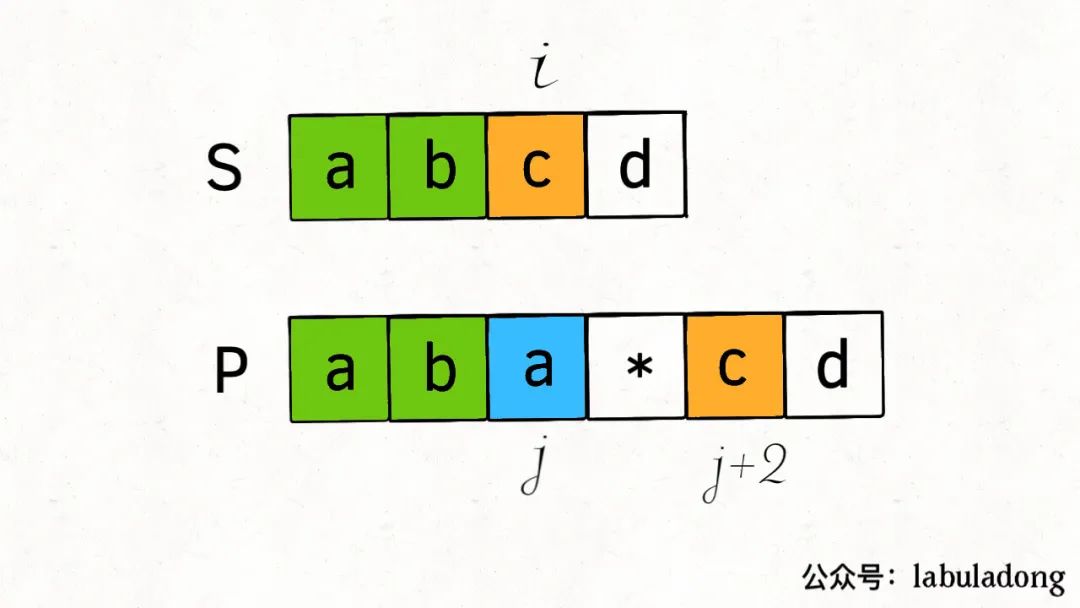
将i加 1，j不变，含义就是p[j]匹配了s[i]，但p[j]还可以继续匹配，即通配符匹配多次的情况：

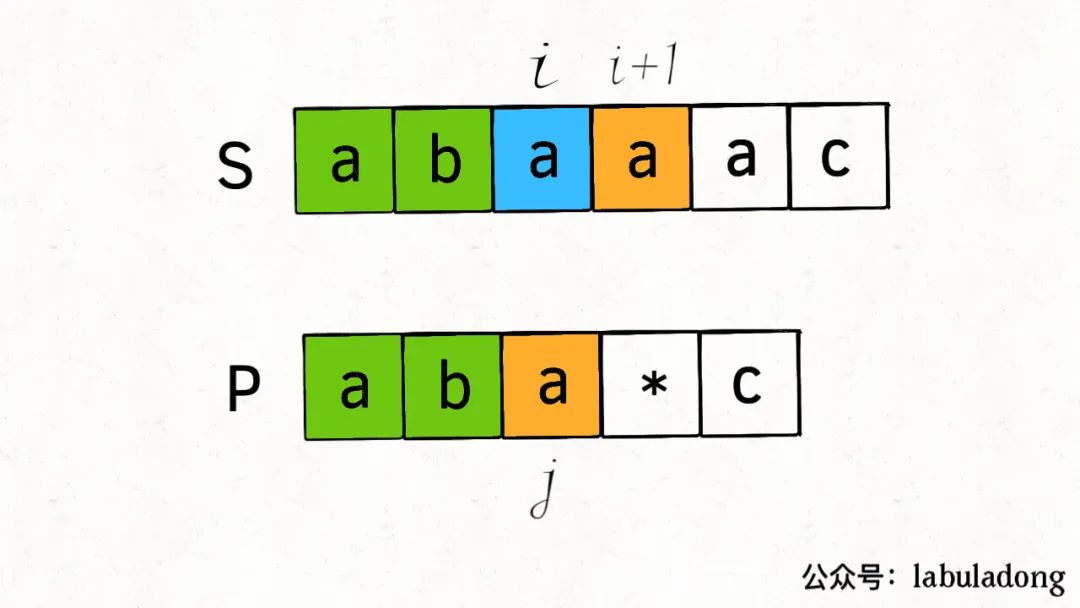
两种情况只要有一种可以完成匹配即可，所以对上面两种情况求或运算。

1.2 常规匹配 1 次

由于这个条件分支是无*的常规匹配，那么如果s[i] == p[j]，就是i和j分别加一：

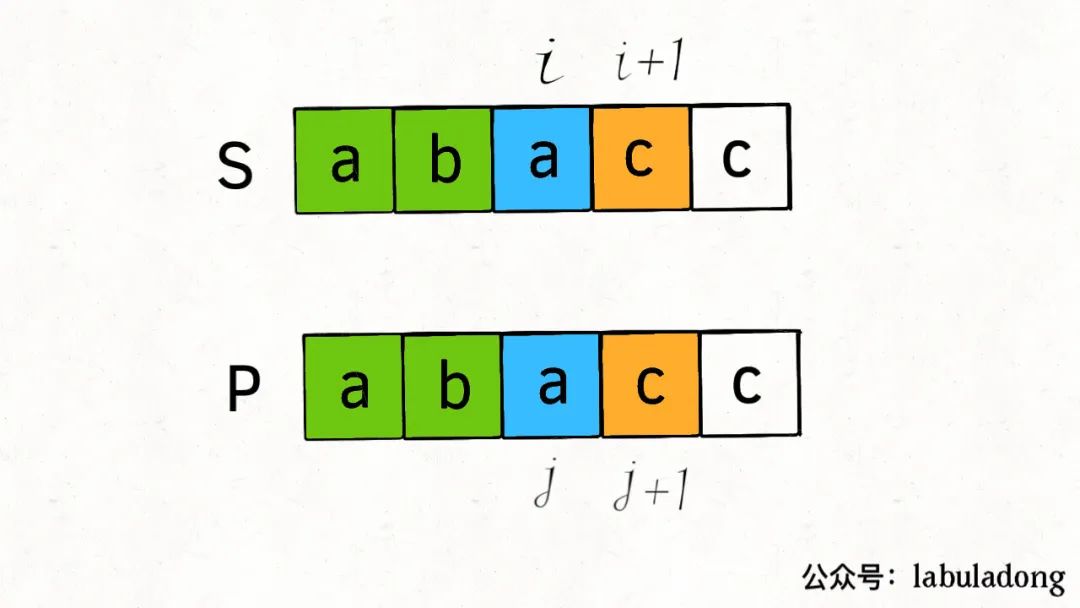
2.1 通配符匹配 0 次

类似情况 1.1，将j加 2，i不变：

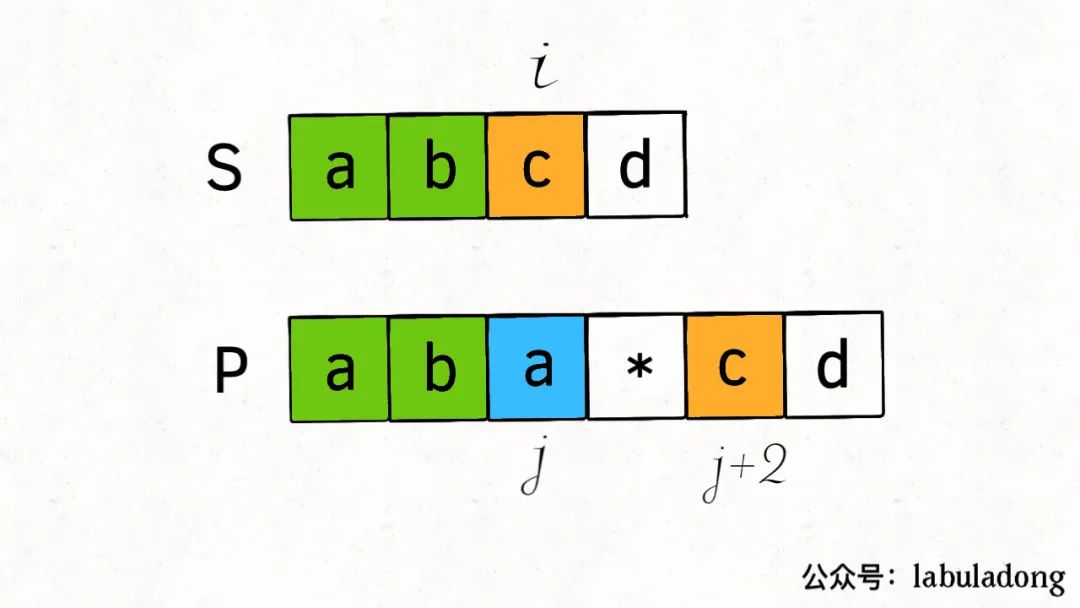
2.2 如果没有*通配符，也无法匹配，那只能说明匹配失败了：

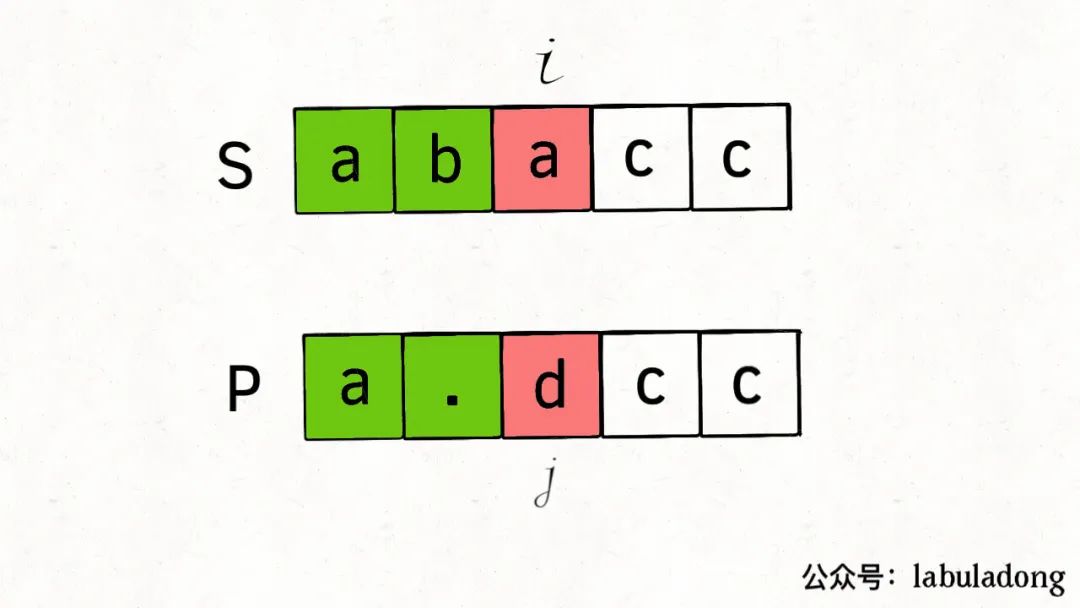
看图理解应该很容易了，现在可以思考一下dp函数的 base case：

一个 base case 是j == p.size()时，按照dp函数的定义，这意味着模式串p已经被匹配完了，那么应该看看文本串s匹配到哪里了，如果s也恰好被匹配完，则说明匹配成功：

1
2
3
if (j == p.size()) {
    return i == s.size();
}

另一个 base case 是i == s.size()时，按照dp函数的定义，这种情况意味着文本串s已经全部被匹配了，那么是不是只要简单地检查一下p是否也匹配完就行了呢？

1
2
3
4
if (i == s.size()) {
    // 这样行吗？
    return j == p.size();
}

这是不正确的，此时并不能根据j是否等于p.size()来判断是否完成匹配，只要p[j..]能够匹配空串，就可以算完成匹配。比如说s = "a", p = "ab*c*"，当i走到s末尾的时候，j并没有走到p的末尾，但是p依然可以匹配s。

所以我们可以写出如下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int m = s.size(), n = p.size();

if (i == s.size()) {
    // 如果能匹配空串，一定是字符和 * 成对儿出现
    if ((n - j) % 2 == 1) {
        return false;
    }
    // 检查是否为 x*y*z* 这种形式
    for (; j + 1 < p.size(); j += 2) {
        if (p[j + 1] != '*') {
            return false;
        }
    }
    return true;
}

综上，完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
public:
    bool isMatch(string s, string p) {
        return dp(s, 0, p, 0);
    }
    // 备忘录
    unordered_map<string, bool> memo;
    bool dp(string& s, int i, string& p, int j){
        int m = s.size(), n = p.size();
        //base case
        if(j == n){
            return i == m;
        }
        if(i == m){
            // 如果能匹配空串，一定是字符和 * 成对儿出现
            if((n - j) % 2 == 1){
                return false;
            }
            //检查是否为 x*y*z* 这种形式
            for(; j + 1 < n; j += 2){
                if(p[j + 1] != '*'){
                    return false;
                }
            }
            return true;
        }

        // 记录状态 (i,j) 消除重叠子问题
        string key = to_string(i) + "," + to_string(j);
        if(memo.count(key)) return memo[key];

        bool res = false;

        if(s[i] == p[j] || p[j] == '.'){
            // 匹配
            if(j < n - 1 && p[j + 1] == '*'){
                // 1.1 通配符匹配 0 次或多次
                res = dp(s, i, p, j + 2) || dp(s, i + 1, p, j);
            }else{
                // 1.2 常规匹配 1 次
                res = dp(s, i + 1, p, j + 1);
            }
        }else{
            // 不匹配
            if(j < n - 1 && p[j + 1] == '*'){
                // 2.1 通配符匹配 0 次
                res = dp(s, i, p, j + 2);
            }else{
                // 2.2 无法继续匹配
                res = false;
            }
        }
        memo[key] = res;
        return res;
    }
};