最长递增子序列

发表于 分类于 ， 阅读次数： Waline： 本文字数： 2.6k 阅读时长 ≈ 2 分钟

300. 最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例：

输入：nums = [10,9,2,5,3,7,101,18]

输出：4

解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

思路：

动态规划解法

dp[i]表示以nums[i]这个数结尾的最长递增子序列的长度

根据这个定义，我们就可以推出 base case：dp[i]的初始值为 1，因为以nums[i]结尾的最长递增子序列起码要包含自己。

index 0 1 2 3 4
nums 1 4 3 4 2

dp[3] = 3

index 0 1 2 3 4
nums 1 4 3 4 2

dp[4] = 2

递推关系，我们只要找到前面比nums[i]小的子序列，然后把nums[i]接到后面，就可以形成一个新的递推增子序列，而且这个新的子序列长度加1

所以可以写出:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        //base case: dp 数组全都初始化为 1
        vector<int> dp(nums.size(),1);
        
        for(int i = 0; i < nums.size(); i++){
            for(int j = 0; j < i; j++){
                if(nums[i] > nums[j]){
                    //找到前面比自己小的递增子序列
                    dp[i] = max(dp[i], dp[j] + 1);
                }
            }
        }
        //取最长递增子序列
        int res = 0;
        for(int i = 0; i < dp.size(); i++){
            res = max(res, dp[i]);
        }
        return res;
    }
};

⾄此，这道题就解决了，时间复杂度O(N^2)，可以看出时间复杂度还很高，我们有没有办法降低。

二分查找法

时间复杂度为O(NlogN)

根据题⽬的意思，我都很难想象这个问题竟然能和⼆分查找扯上关系。其实最⻓递增⼦序列和⼀种叫做patience game 的纸牌游戏有关，甚⾄有⼀种排序⽅法就叫做 patience sorting（耐⼼排序）。

⾸先，给你⼀排扑克牌，我们像遍历数组那样从左到右⼀张⼀张处理这些扑克牌，最终要把这些牌分成若⼲堆。

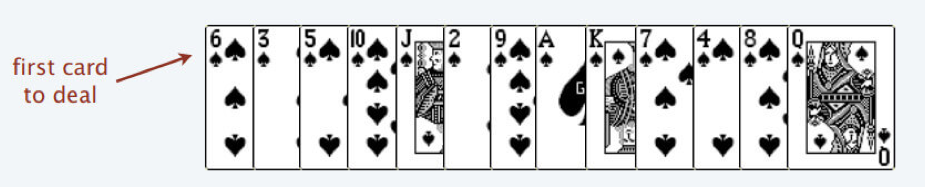
处理这些扑克牌要遵循以下规则：

只能把点数⼩的牌压到点数⽐它⼤的牌上；如果当前牌点数较⼤没有可以放置的堆，则新建⼀个堆，把这张牌放进去；如果当前牌有多个堆可以选择，则选择最左边的那一堆放置。

⽐如说上述的扑克牌最终会被分成这样 5 堆（我们认为纸牌 A 的牌⾯是最⼤的，纸牌 2 的牌⾯是最⼩的）。

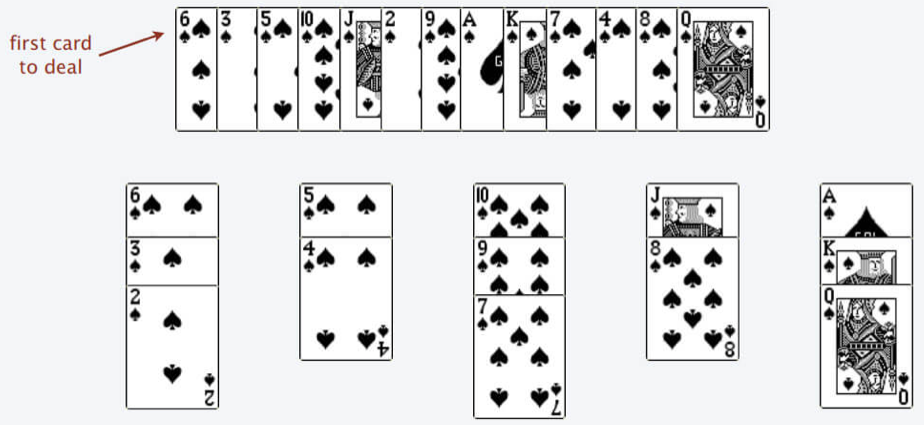
为什么遇到多个可选择堆的时候要放到最左边的堆上呢？因为这样可以保证牌堆顶的牌有序（2, 4, 7, 8，Q）

按照上述规则执⾏，可以算出最⻓递增⼦序列，牌的堆数就是最⻓递增⼦序列的⻓度，证明略。

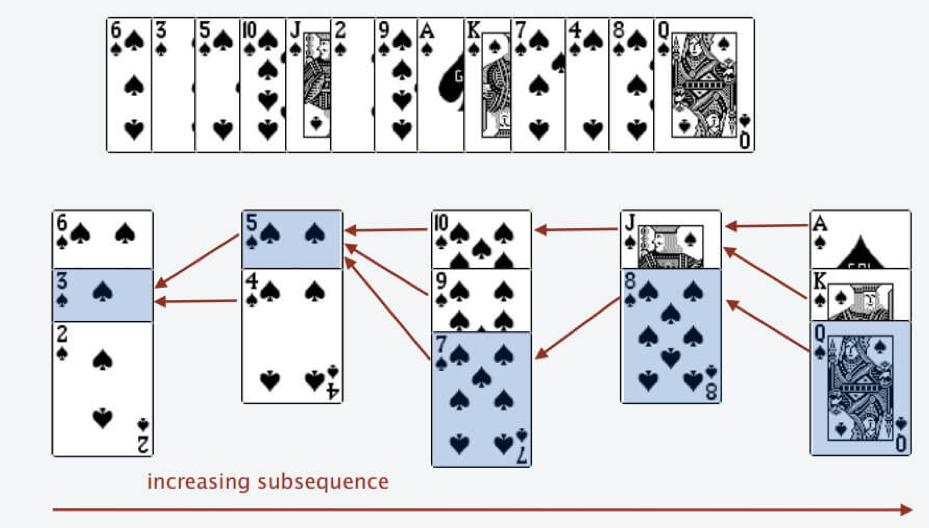
我们只要把处理扑克牌的过程编程写出来即可。每次处理⼀张扑克牌不是要找⼀个合适的牌堆顶来放吗，牌堆顶部的牌不就是有序吗？

这就能用到二分查找了：==用二分查找来搜索当前牌应放置的位置。==

最长递增子序列的个数就是堆牌的个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> top(nums.size(), 0);
        // 牌堆数初始化为0
        int piles = 0;
        for(int i = 0; i < nums.size(); i++){
            // 想要处理的扑克牌
            int poker = nums[i];

            // 搜索左侧边界的二分查找
            int left = 0, right = piles;
            while(left < right){
                int mid = (left + right) / 2;
                if(top[mid] > poker){
                    right = mid;
                }else if(top[mid] < poker){
                    left = mid + 1;
                }else{
                    right = mid;
                }
            }

            // 没找到合适的牌堆，新建一堆
            if(left == piles) piles++;
            // 把这张牌放到牌堆顶
            top[left] = poker;
        }
        return piles;
    }
};