给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列
的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列
是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
思路:
对于两个字符串求子序列的问题,都是用两个指针i和j分别在两个字符串上移动,大概率是动态规划思路。
我们定义一个dp[i][j]表示:s1[0...i-1]和s2[0...j-1]的
LCS的长度为 dp[i][j]
接下来,咱不要看s1和s2两个字符串,而是要具体到每一个字符,思考每个字符该做什么。
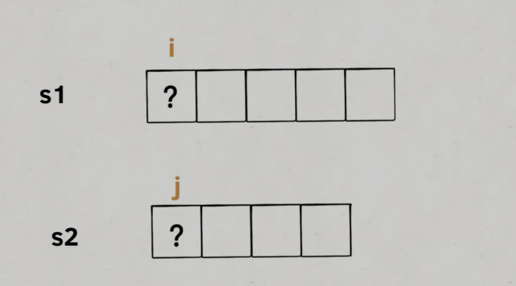
我们只看s1[i]和s2[j],如果s1[i] == s2[j],说明这个字符一定在lcs中:

这样,就找到了一个lcs中的字符,根据dp函数的定义,我们可以完善一下代码:
1
2
3
| if(s1[i] == s2[j]){
dp[i][j] = dp[i-1][j-1] + 1;
}
|
如果s1[i] != s2[j],意味着,s1[i]和s2[j]中至少有一个字符不在lcs中:
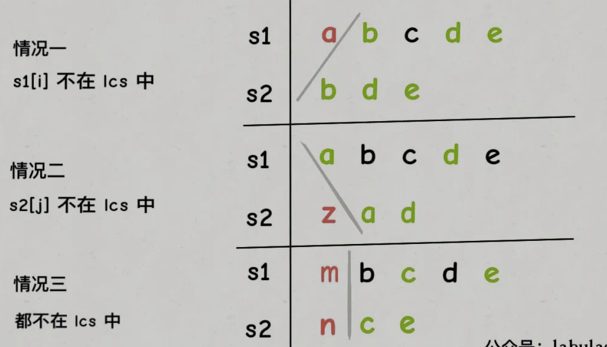
我们只需要计算这三种情况中的最大值。
可以发现情况三其实可以忽略,因为我们要求的是最长公共子序列,情况一和情况二肯定会比情况三长。
1
2
3
| if(s1[i] != s2[j]){
dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
}
|
完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int m = text1.size(), n = text2.size();
vector<vector<int> > dp(m + 1, vector<int> (n + 1, 0));
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(text1[i - 1] == text2[j - 1]){
dp[i][j] = dp[i - 1][j - 1] + 1;
}else{
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
return dp[m][n];
}
};
|
为了加深理解,我们可以自己手推一下dp数组。
假设s1 = abecbab,s2 = bdcbabb
相等时,dp[i][j] = dp[i-1][j-1] + 1,也就是左上角元素➕1
不等时,dp[i][j] = max(dp[i-1][j], dp[i][j-1]),左边和上边的最大值
| b |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
| d |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
| c |
0 |
1 |
1 |
2 |
2 |
2 |
2 |
| b |
0 |
1 |
1 |
2 |
3 |
3 |
3 |
| a |
1 |
1 |
1 |
2 |
3 |
4 |
4 |
| b |
1 |
2 |
2 |
2 |
3 |
4 |
5 |
| b |
1 |
2 |
2 |
2 |
3 |
4 |
5 |
所以最终我们的结果就为dp[m][n] = 5
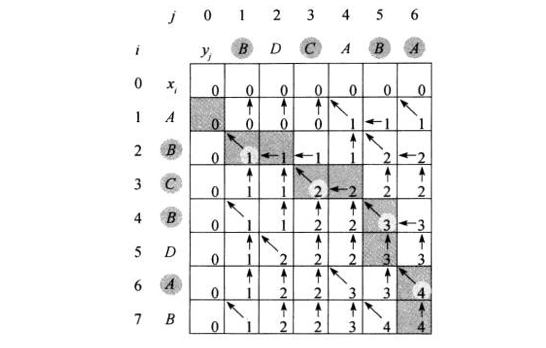
现在我们求出了最长公共子序列的长度,假如需要我们输出任意一个路径,我们应该如何写呢?
这里我们先简单的提一下思路:
我们可以根据我们得到的dp数组,从后往前递推。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
| #include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef vector<int> vi;
string s1,s2;
vector<vector<int> > dp;
unordered_set<string> lcs;
int longestCommonSubsequence(string text1, string text2) {
int n = text1.size(), m = text2.size();
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
if(text1[i - 1] == text2[j - 1]){
dp[i][j] = 1 + dp[i - 1][j - 1];
}else{
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
return dp[n][m];
}
void print_lcs(int i, int j, string lcs_str){
while(i > 0 && j > 0){
if(s1[i-1] == s2[j-1]){
lcs_str.push_back(s1[i-1]);
--i;
--j;
}else{
if(dp[i-1][j] > dp[i][j-1]) --i;
else if(dp[i-1][j] < dp[i][j-1]) --j;
else{
print_lcs(i-1,j,lcs_str);
print_lcs(i,j-1,lcs_str);
return;
}
}
}
reverse(lcs_str.begin(), lcs_str.end());
lcs.insert(lcs_str);
}
int main(){
s1 = "abcbdab";
s2 = "bdcaba";
int s1_len = s1.size();
int s2_len = s2.size();
dp.resize(s1_len + 1, vector<int>(s2_len + 1, 0));
int res = longestCommonSubsequence(s1,s2);
cout << res << "\n";
string str;
print_lcs(s1_len,s2_len,str);
unordered_set<string>::iterator it = lcs.begin();
for(; it != lcs.end(); it++){
cout << *it << endl;
}
return 0;
}
|



