单链表的基本技巧:
1,合并两个有序链表
2,合并 K 个有序链表
3,寻找单链表的倒数第 K 个节点
4,寻找单链表的中点
5,判断单链表是否包含环并找出环起点
6,判断两个单链表是否相交并找出交点
1,合并两个有序链表
将两个升序链表合并为一个新的 升序
链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例:
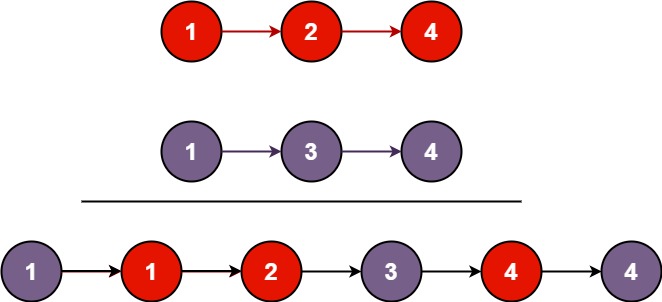
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
思路:
对于两个升序的链表,我们首先想到的肯定是归并排序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
ListNode* dummy = new ListNode(-1);
ListNode* p = dummy;
ListNode* p1 = list1;
ListNode* p2 = list2;
while(p1 != nullptr && p2 != nullptr){
if(p1->val > p2->val){
p->next = p2;
p2 = p2->next;
}else{
p->next = p1;
p1 = p1->next;
}
p = p->next;
}
if(p1 != nullptr){
p->next = p1;
}
if(p2 != nullptr){
p->next = p2;
}
return dummy->next;
}
};
|
2,合并 K 个有序链表
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下: []
将它们合并到一个有序链表中得到。 >
1->1->2->3->4->4->5->6
思路:
方法一:归并排序
我们是不是可以转化为前面我们说过的两个队列,然后依次合并即可。
那么我们应该如何转化呢,可以定义一个空的链表,依次合并。
时间复杂度为:O(NlogN);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
ListNode* dummy = nullptr;
for(int i = 0; i < lists.size(); i++){
ListNode* t = mergeTwoLists(dummy, lists[i]);
dummy = t;
}
return dummy;
}
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2){
ListNode* node = new ListNode(-1);
ListNode* cur = node;
while(l1 != nullptr && l2 != nullptr){
if(l1->val < l2->val){
cur->next = l1;
l1 = l1->next;
}else{
cur->next = l2;
l2 = l2->next;
}
cur = cur->next;
}
if(l1 != nullptr){
cur->next = l1;
}
if(l2 != nullptr){
cur->next = l2;
}
return node->next;
}
};
|
方法二: 优先队列(二叉堆)
把链表节点放入一个最小堆中,就可以每次获得 K 个节点中的最小节点。
时间复杂度为:O(NlogK)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public:
static bool myCmp(ListNode* l1, ListNode* l2) {
return l1->val >= l2->val;
}
ListNode* mergeKLists(vector<ListNode*>& lists) {
if(lists.size() == 0) return nullptr;
ListNode* dummy = new ListNode(-1);
ListNode* p = dummy;
priority_queue<ListNode*, vector<ListNode*>, function<bool(ListNode*, ListNode*)>> pq(myCmp);
for(ListNode* head : lists){
if(head != nullptr)
pq.push(head);
}
while(!pq.empty()){
ListNode* node = pq.top();
pq.pop();
p->next = node;
if(node->next != nullptr){
pq.push(node->next);
}
p = p->next;
}
return dummy->next;
}
};
|
优先队列pq中的元素个数最多是k,所以一次push或者pop方法的时间复杂度是O(logk);所有的链表节点都会被加入和弹出pq,所以算法整体的时间复杂度是O(Nlogk),其中k是链表的条数,N是这些链表的节点总数。
3,寻找单链表的倒数第 K 个节点
给你一个链表,删除链表的倒数第 n
个结点,并且返回链表的头结点。
示例:
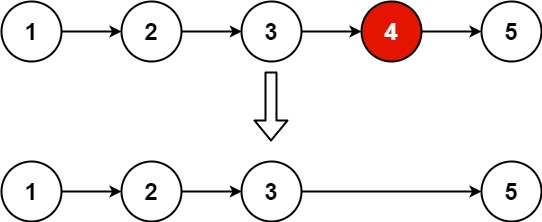
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
思路:
我们要想删除单链表中的一个节点,我们需要知道这个节点的前一个节点。
那么我们该如何找到这个节点呢?这就需要双指针,
先设置p1先走k+1步,然后p2从头节点同时走,这样p1走到结尾,p2就是我们要找的节点。
例如:
1->2->3->4->5
n = 2
也就是要删除4,我们需要找到3,也就是倒数第n+1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummy = new ListNode(-1);
dummy->next = head;
ListNode* x = findFromEnd(dummy, n + 1);
x->next = x->next->next;
return dummy->next;
}
ListNode* findFromEnd(ListNode* head, int k){
ListNode* p1 = head;
for(int i = 0; i < k; i++){
p1 = p1->next;
}
ListNode* p2 = head;
while(p1 != nullptr){
p2 = p2->next;
p1 = p1->next;
}
return p2;
}
};
|
不过注意我们又使用了虚拟头结点的技巧,也是为了防止出现空指针的情况,比如说链表总共有
5 个节点,题目就让你删除倒数第 5
个节点,也就是第一个节点,那按照算法逻辑,应该首先找到倒数第 6
个节点。但第一个节点前面已经没有节点了,这就会出错。
但有了我们虚拟节点dummy的存在,就避免了这个问题,能够对这种情况进行正确的删除。
4,寻找单链表的中点
给定一个头结点为 head
的非空单链表,返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
示例:
输入:[1,2,3,4,5]
输出:此列表中的结点 3 (序列化形式:[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
注意,我们返回了一个 ListNode 类型的对象 ans,这样:
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及
ans.next.next.next = NULL.
思路:
找中间节点,需要用到快慢指针,慢指针走一步,快指针走两步。
最后返回慢指针即可。
1
2
3
4
5
6
7
8
9
10
11
| class Solution {
public:
ListNode* middleNode(ListNode* head) {
ListNode *slow = head,*fast = head;
while(fast != nullptr && fast->next != nullptr){
slow = slow->next;
fast = fast->next->next;
}
return slow;
}
};
|
需要注意的是,如果链表长度为偶数,也就是说中点有两个的时候,我们这个解法返回的节点是靠后的那个节点。
5, 判断是否有环以及环的起点
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next
指针再次到达,则链表中存在环。
为了表示给定链表中的环,评测系统内部使用整数 pos
来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos
不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例:
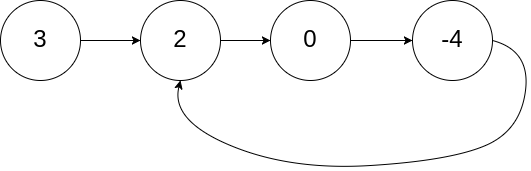
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
思路:
判断单链表是否包含环属于经典问题了,解决方案也是用快慢指针:
每当慢指针slow前进一步,快指针fast就前进两步。
如果fast最终遇到空指针,说明链表中没有环;如果fast最终和slow相遇,那肯定是fast超过了slow一圈,说明链表中含有环。
只需要把寻找链表中点的代码稍加修改就行了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public:
bool hasCycle(ListNode *head) {
ListNode *slow = head, *fast = head;
while(fast != nullptr && fast->next != nullptr){
slow = slow->next;
fast = fast->next->next;
if(slow == fast){
return true;
}
}
return false;
}
};
|
进阶的话就是问环的起点。
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。
如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next
指针再次到达,则链表中存在环。
为了表示给定链表中的环,评测系统内部使用整数 pos
来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是
-1,则在该链表中没有环。注意:pos
不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。

示例:
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
思路:
我们用前面的算法判断了是否有环。
我们假设快慢指针相遇时,慢指针slow走了k步,那么快指针fast一定走了2k步:
ps: 因为慢指针走一步,快指针走两步
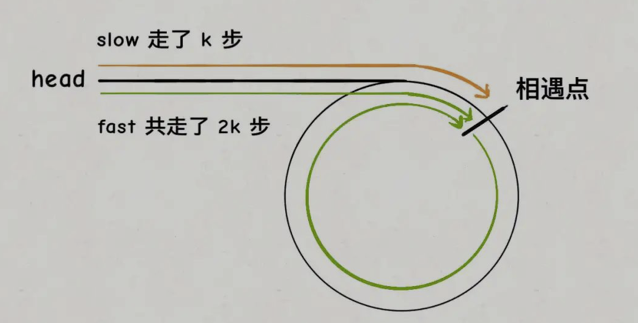
fast一定比slow多走了k步,这多走的k步其实就是fast指针在环里转圈圈,所以k的值就是环长度的「整数倍」。
假设相遇点距环的起点的距离为m,那么结合上图的 slow
指针,环的起点距头结点head的距离为k - m,也就是说如果从head前进k - m步就能到达环起点。
巧的是,如果从相遇点继续前进k - m步,也恰好到达环起点。因为结合上图的
fast
指针,从相遇点开始走k步可以转回到相遇点,那走k - m步肯定就走到环起点了:
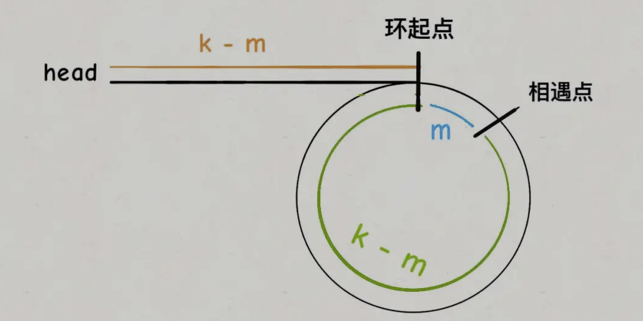
所以,只要我们把快慢指针中的任一个重新指向head,然后两个指针同速前进,k - m步后一定会相遇,相遇之处就是环的起点了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *slow, *fast;
slow = fast = head;
while(fast != nullptr && fast->next != nullptr){
fast = fast->next->next;
slow = slow->next;
if(slow == fast) break;
}
if(fast == nullptr || fast->next == nullptr){
return nullptr;
}
slow = head;
while(slow != fast){
fast = fast->next;
slow = slow->next;
}
return slow;
}
};
|
6,判断两个单链表是否相交并找出交点
给你两个单链表的头节点 headA 和 headB
,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回
null 。
图示两个链表在节点 c1 开始相交:
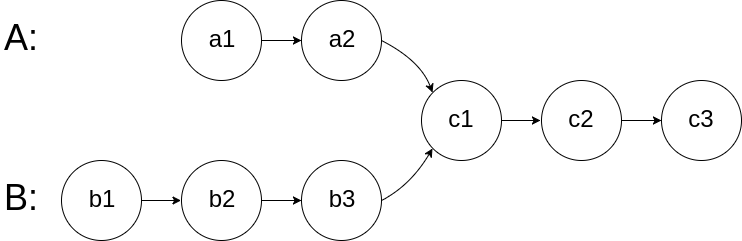
示例:
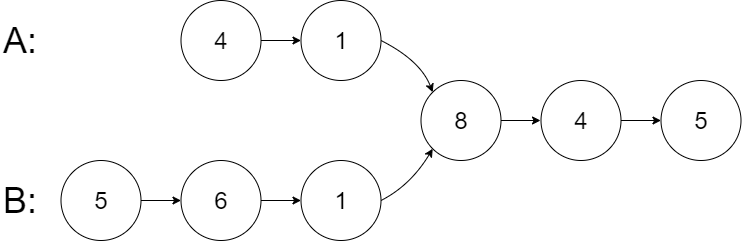
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5],
skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为
[5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
思路:
方法一:
我们可以让两个链表同时到终点,也就是说如果我们知道headA和headB的长度,让长度长的走lenA - lenB(假设A的长度长)然后判断是否是同一个链表,如果是就返回,不是就同时前进。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int lenA = 0, lenB = 0;
for(ListNode* p1 = headA; p1 != nullptr; p1 = p1->next){
lenA++;
}
for(ListNode* p2 = headB; p2 != nullptr; p2 = p2->next){
lenB++;
}
ListNode* p1 = headA, *p2 = headB;
if(lenA > lenB){
for(int i = 0; i < lenA - lenB; i++){
p1 = p1->next;
}
}else{
for(int i = 0; i < lenB - lenA; i++){
p2 = p2->next;
}
}
while(p1 != p2){
p1 = p1->next;
p2 = p2->next;
}
return p1;
}
};
|
方法二:
我们可以把headA的尾指针指向头节点,这样不就转化为前面所说过的求环的起点了吗?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode *p1 = headA;
while(p1->next != nullptr){
p1 = p1->next;
}
p1->next = headA;
ListNode *slow, *fast;
slow = headB, fast = headB;
while(fast != nullptr && fast->next != nullptr){
slow = slow->next;
fast = fast->next->next;
if(slow == fast){
break;
}
}
if(fast == nullptr || fast->next == nullptr){
return nullptr;
}
slow = headB;
while(slow != fast){
slow = slow->next;
fast = fast->next;
}
return slow;
}
};
|







