区间问题

发表于 分类于 ， 阅读次数： Waline： 本文字数： 5k 阅读时长 ≈ 5 分钟

区间问题就是线段问题，让你合并所有线段，找出线段的交集等。主要有两个技巧：

1，排序： 常见的排序方法就是按照区间起点排序，或者先按照起点升序排序，若起点相同，则按照终点降序排列。

2，画图： 画图可以更直观的看出两个区间的相对位置到底有几种可能，不同的相对位置，我们应该如何去解决。

1288. 删除被覆盖区间

给你一个区间列表，请你删除列表中被其他区间所覆盖的区间。

只有当 c <= a 且 b <= d 时，我们才认为区间 [a,b) 被区间 [c,d) 覆盖。

在完成所有删除操作后，请你返回列表中剩余区间的数目。

示例：

输入：intervals = [[1,4],[3,6],[2,8]]

输出：2

解释：区间 [3,6] 被区间 [2,8] 覆盖，所以它被删除了。

思路：

我们可以先算出被覆盖的区间有几个，最后再用总数减去即可。

第一步，我们先排序：

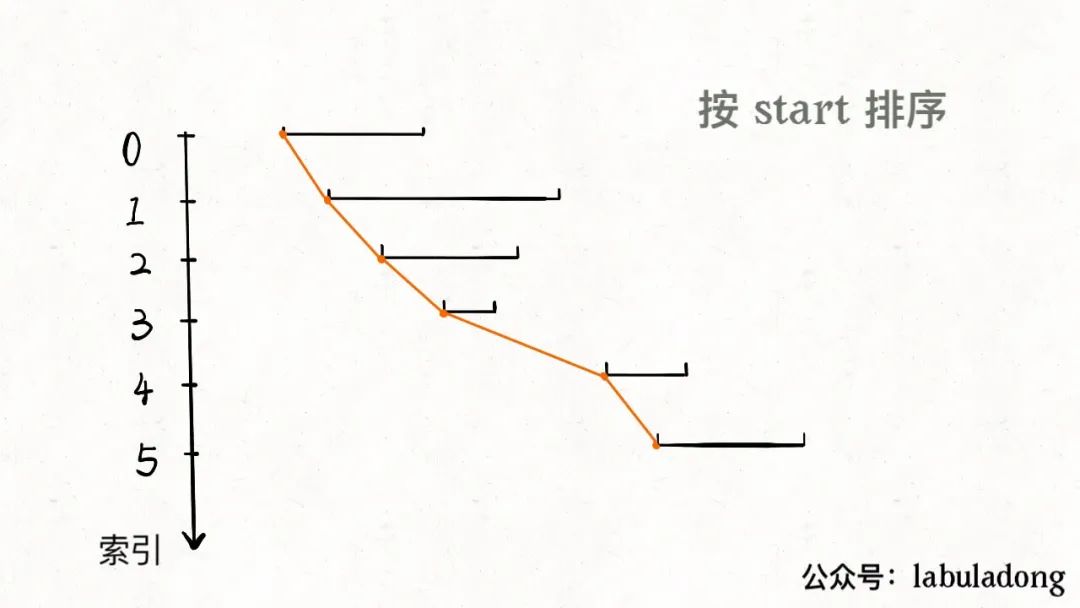
排序之后，两个相邻区间可能有如下三种相对位置：

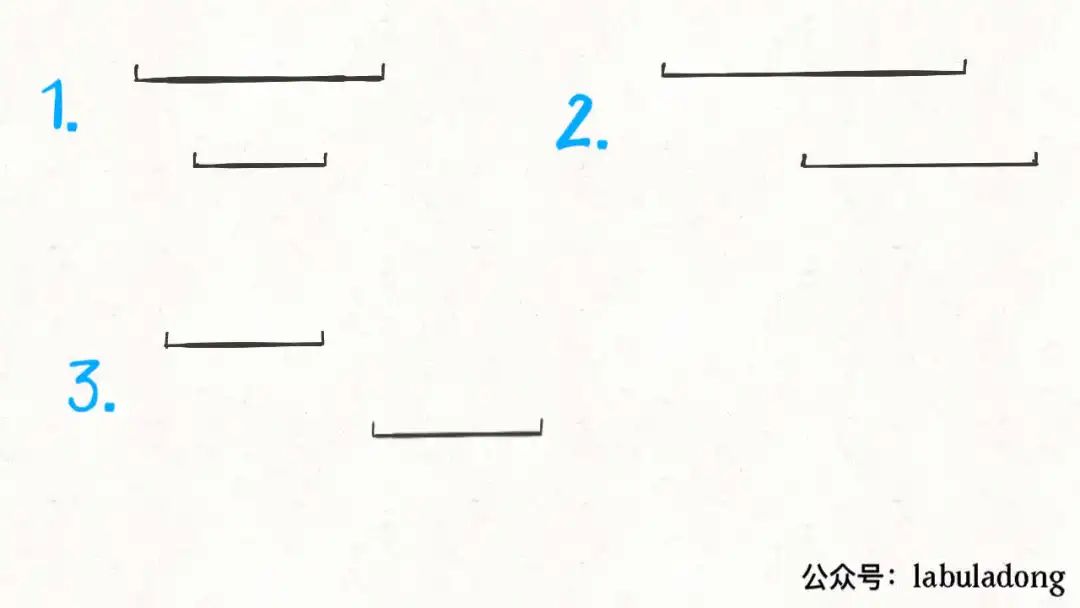
对于这三种情况，我们应该这样处理：

对于情况一，找到了覆盖区间。

对于情况二，两个区间可以合并，成一个大区间。

对于情况三，两个区间完全不相交。

所以代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    int removeCoveredIntervals(vector<vector<int> >& intervals) {
        //按照起点升序排列，起点相同时降序排列
        sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){
            if(a[0] == b[0]){
                return a[1] > b[1];
            }
            return a[0] < b[0];
        });

        //记录合并区间的起点和终点
        int left = intervals[0][0];
        int right = intervals[0][1];

        int res = 0;
        for(int i = 1; i < intervals.size(); i++){
            vector<int> intv = intervals[i];
            //情况一，找到覆盖区间
            if(left <= intv[0] && right >= intv[1]){
                res++;
            }
            //情况二，找到相交区间，合并
            if(right >= intv[0] && right <= intv[1]){
                right = intv[1];
            }
            //情况三，完全不相交
            if(right < intv[0]){
                left = intv[0];
                right = intv[1];
            }
        }
        return intervals.size() - res;
    }
};

56. 合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]

输出：[[1,6],[8,10],[15,18]]

解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

思路：

我们解决区间问题一般是先排序，然后画图。我们按照起点升序排序，得到以下图形。

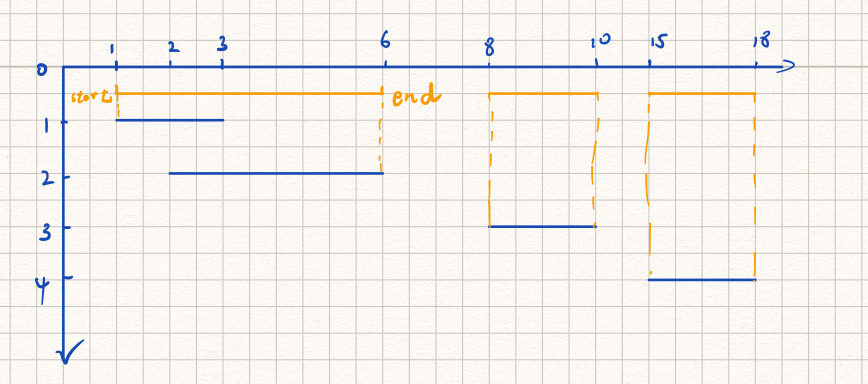
显然，对于相交的线段，最小的起点就是start最小的，end为其中结尾最大的。那问题就转化为找到相交中起点最小的和终点最大的，

由于我们已经按照起点排序了，那么第一位就是我们的start,那么end应该如何确定呢，我们只需要判断下一个要来的起点是否小于当前的终点，如果小于，那么终点就是这两个结尾的最大值。

例如[1,3]和[2,6]，2 < 3 所以必相交，终点就更新为max(3, 6) = 6；

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<vector<int> > merge(vector<vector<int> >& intervals) {
        sort(intervals.begin(), intervals.end());

        vector<vector<int> > res;
        res.push_back(intervals[0]);
        for(int i = 1; i < intervals.size(); i++){
            vector<int> curr = intervals[i];
            // res 中最后一个元素的引用
            vector<int> last = res.back();
            //后一个开始节点小于前一个的终点，所以相交或覆盖，取两条线段尾部最大的
            if(curr[0] <= last[1]){
                last[1] = max(last[1], curr[1]);
              	//更新终点
                res.pop_back();
                res.push_back(last);
            }else{
                //处理下一个待合并的区间
                res.push_back(curr);
            }
        }
        return res;
    }
};

986. 区间列表的交集

给定两个由一些 闭区间 组成的列表，firstList 和 secondList ，其中 firstList[i] = [starti, endi] 而 secondList[j] = [startj, endj] 。每个区间列表都是成对 不相交 的，并且 已经排序 。

返回这 两个区间列表的交集 。

形式上，闭区间 [a, b]（其中 a <= b）表示实数 x 的集合，而 a <= x <= b 。

两个闭区间的 交集 是一组实数，要么为空集，要么为闭区间。例如，[1, 3] 和 [2, 4] 的交集为 [2, 3] 。

示例：

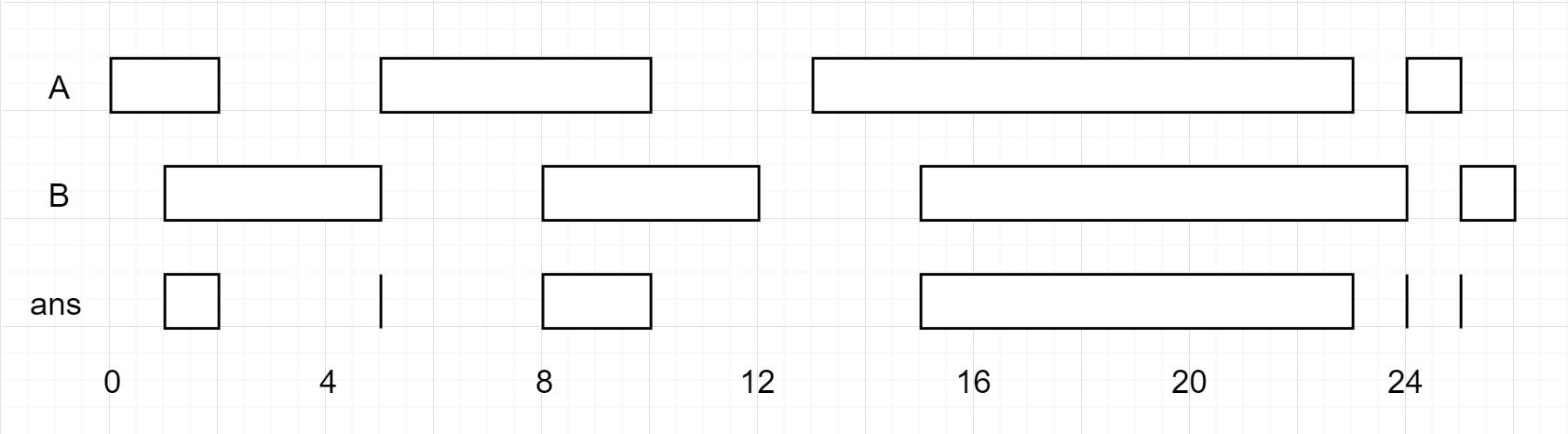
输入：firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]

输出：[[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

思路：

第一步，排序，已经排过序了，那我们使用双指针。

我们分析下各种情况：

  • 对于两个区间，我们用[a1,a2]和[b1,b2]表示在A 和 B中的两个区间，那么什么时候没有交集呢？

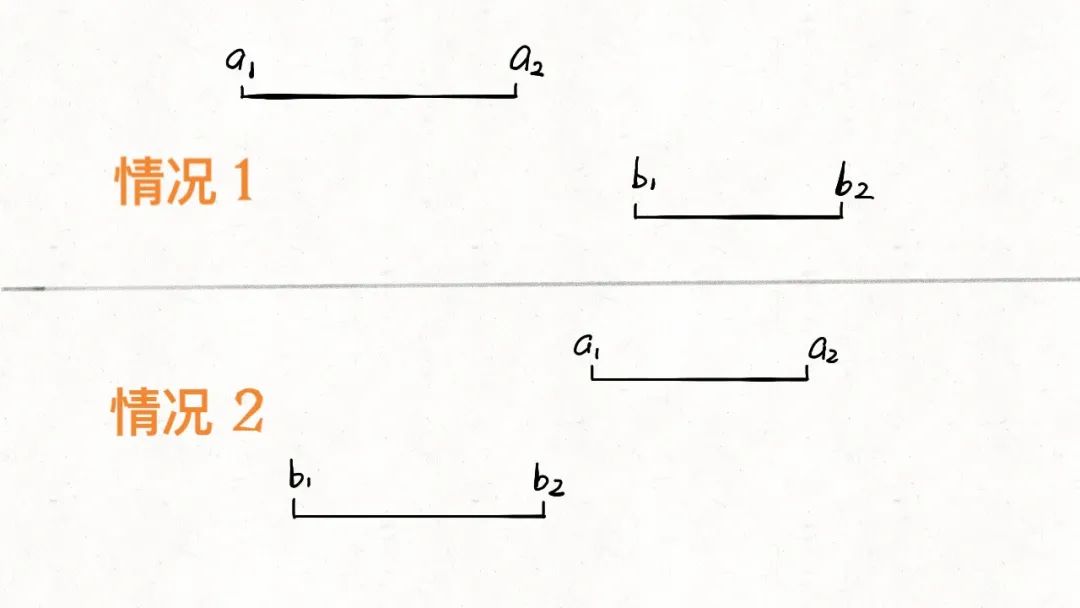
只有这两种情况：

1
2
3
if(b2 < a1 || a2 < b1){
	[a1,a2]和[b1,b2]无交集
}

那么什么时候存在交集呢？根据命题的否定

1
2
3
if(b2 >= a1 && a2 >= b1){
	存在交集
}

穷举出来如下：

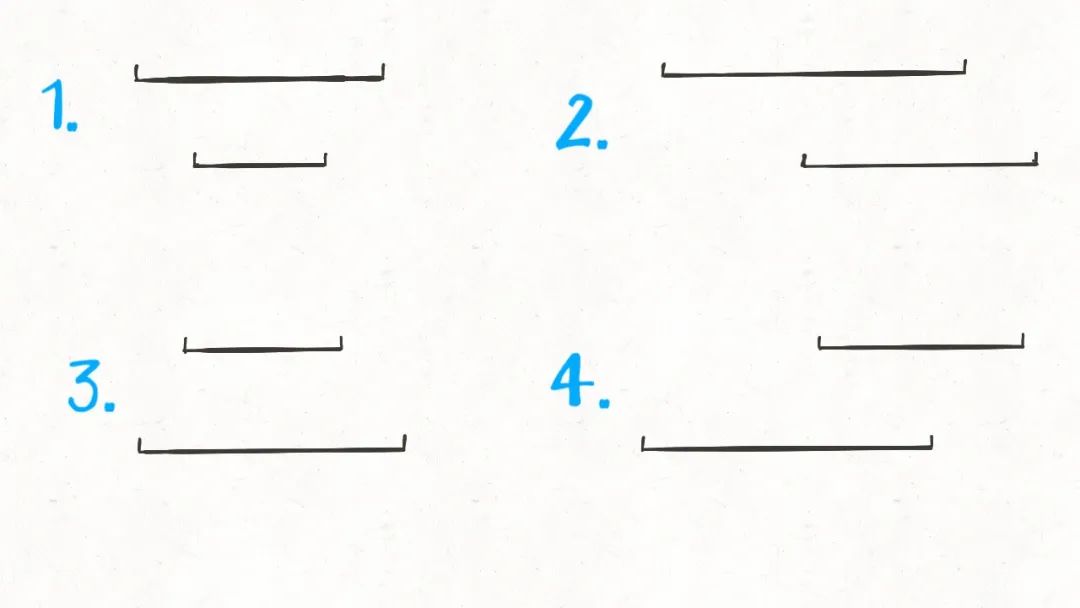
这很简单吧，就这四种情况而已。那么接下来思考，这几种情况下，交集是否有什么共同点呢？

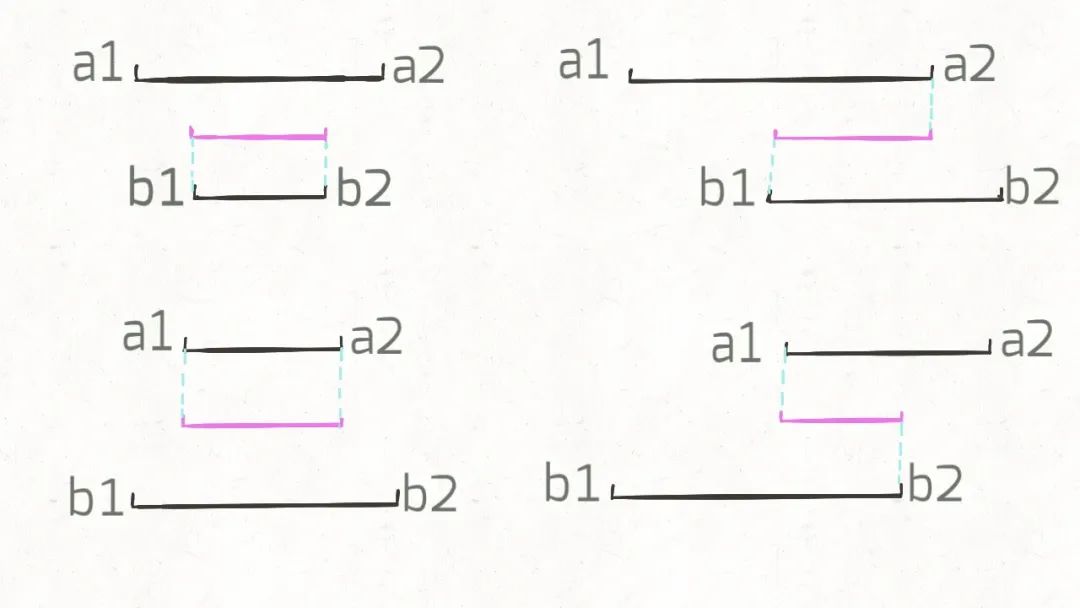
我们惊奇地发现，交集区间是有规律的！如果交集区间是[c1,c2]，那么c1=max(a1,b1)，c2=min(a2,b2)！这一点就是寻找交集的核心，我们把代码更进一步：

1
2
3
4
5
6
while i < len(A) and j < len(B):
    a1, a2 = A[i][0], A[i][1]
    b1, b2 = B[j][0], B[j][1]
    if b2 >= a1 and a2 >= b1:
        res.append([max(a1, b1), min(a2, b2)])
    # ...

最后一步，我们的指针 i和j什么时候前进？

我们发现当 b2 < a2时，我们的j会往前，因为此时这个线段的最长已经在A的里面了。

同理当 b2 >= a2 时， i++;

所以，完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<vector<int> > intervalIntersection(vector<vector<int> >& firstList, vector<vector<int> >& secondList) {
        if(firstList.size() == 0) return {};
        if(secondList.size() == 0) return {};

        int i  = 0, j = 0;
        vector<vector<int> > res;
        while(i < firstList.size() && j < secondList.size()){
            int a1 = firstList[i][0];
            int a2 = firstList[i][1];

            int b1 = secondList[j][0];
            int b2 = secondList[j][1];

            //两个区间存在交集
            if(b2 >= a1 && a2 >= b1){
                //计算出交集，加入res
                res.push_back({max(a1,b1), min(a2,b2)});
            }
            //指针前进
            if(b2 < a2) j += 1;
            else i += 1;
        }
        return res;
    }
};