剑指offer

发表于 2022-08-14 分类于算法，剑指offer 阅读次数： Waline：本文字数： 45k 阅读时长 ≈ 41 分钟

剑指offer

06.从尾到头打印链表

输入一个链表的头节点，从尾到头反过来返回每个节点的值（用数组返回）。

示例：

输入：head= 【1，3，2】

输出：[2,3,1]

方法一：遍历翻转

借助栈的后进先出特性来实现

class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        vector<int>res;
        while(head){
            res.push_back(head->val);
            head = head->next;
        }
        reverse(res.rbegin(),res.rend());
        return res;
    }
};

方法二：递归法

先走到链表末端，回溯时依次将节点值加入列表，这样就可以实现链表的倒叙输出

class Solution {
public:
    vector<int>res;
    vector<int> reversePrint(ListNode* head) {
        if(head!=NULL){
            if(head->next!=NULL){
                reversePrint(head->next);
            }
            res.push_back(head->val);
        }
        return res;
    }
};

07. 重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例：

输入：preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

输出：[3,9,20,null,null,15,7]

解题思路：

前序遍历性质：节点按照 [ 根节点 | 左子树 | 右子树 ] 排序。中序遍历性质：节点按照 [ 左子树 | 根节点 | 右子树 ] 排序。

以题目示例为例：

前序遍历划分 [ 3 | 9 | 20 15 7 ] 中序遍历划分 [ 9 | 3 | 15 20 7 ] 根据以上性质，可得出以下推论：

前序遍历的首元素为树的根节点 node 的值。在中序遍历中搜索根节点 node 的索引，可将中序遍历划分为 [ 左子树 | 根节点 | 右子树 ] 。根据中序遍历中的左（右）子树的节点数量，可将前序遍历划分为 [ 根节点 | 左子树 | 右子树 ] 。

通过以上三步，可确定三个节点：1.树的根节点、2.左子树根节点、3.右子树根节点。

根据「分治算法」思想，对于树的左、右子树，仍可复用以上方法划分子树的左右子树。

分治算法解析：

递推参数：根节点在前序遍历的索引 root 、子树在中序遍历的左边界 left 、子树在中序遍历的右边界 right ；
终止条件：当 left > right ，代表已经越过叶节点，此时返回 null ；
递推工作： 1，建立根节点 node ：节点值为 preorder[root] ； 2，划分左右子树：查找根节点在中序遍历 inorder 中的索引 i ；

为了提升效率，本文使用哈希表 dic 存储中序遍历的值与索引的映射，查找操作的时间复杂度为O(1) ；

构建左右子树：开启左右子树递归；根节点索引中序遍历左边界中序遍历右边界

左子树 root + 1 left i - 1 右子树 i - left + root + 1 i + 1 right

TIPS： i - left + root + 1含义为根节点索引 + 左子树长度 + 1

返回值：回溯返回 node ，作为上一层递归中根节点的左 / 右子节点；

class Solution {
public:
    unordered_map<int,int>mp;
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        //将中序序列用哈希表存储，便于查找根节点
        for(int i=0;i<inorder.size();i++){
            mp[inorder[i]] = i;
        }
        //传入参数：前序、中序、前序序列根节点、中序序列左边界、中序序列右边界
        return recur(preorder,inorder,0,0,inorder.size()-1);
    }

    TreeNode* recur(vector<int>& preorder,vector<int>& inorder,int pre_root,int in_left,int in_right){
        if(in_left > in_right) return NULL;
        //建立新节点
        TreeNode* root = new TreeNode(preorder[pre_root]);
        //根节点在中序序列中的位置，用于划分左右子树的边界
        int in_root = mp[preorder[pre_root]];
        //左子树在前序中的根节点位于：pre_root+1,左子树在中序中的边界：[int_left,in_root-1]
        root->left = recur(preorder,inorder,pre_root+1,in_left,in_root-1);
        // 右子树在前序中的根节点位于：根节点+左子树长度+1 = pre_root+in_root-in_left+1
        // 右子树在中序中的边界：[in_root+1,in_right]
        root->right = recur(preorder,inorder,pre_root+in_root-in_left+1,in_root+1,in_right);
        return root;
    }
};

####09. 用两个栈实现队列

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

示例1:

输入：

["CQueue","appendTail","deleteHead","deleteHead"]

[[],[3],[],[]]

输出：

[null,null,3,-1]

题目理解：

["CQueue","appendTail","deleteHead","deleteHead"] 这里是要执行的方法，从左到右执行

[[],[3],[],[]]对应上面的方法，是上面方法的参数。CQueue和deleteHead方法不需要指定数字，只有添加才需要指定数字

1.创建队列，返回值为null

2.将3压入栈，返回值为null

3.将栈底的元素删除，也就是消息队列中先进来的元素，所以是deleteHead，返回该元素的数值，所以为3

4.继续删除栈底的元素，但是没有元素了，所以返回-1

所以就有了下面的输出输出：[null,null,3,-1]

解题思路：

双栈可以实现列表倒序

1，加入队尾appenTail()函数：将数字val加入栈A

2，删除队首deleteHead()函数：有以下三种情况

1）当栈B不为空时：B中仍有已完成倒序的元素，因此直接返回B的栈顶元素

2）否则，当A为空时：即两个栈都为空，无元素，因此返回-1

3）否则，将栈A元素全部转移至栈B中，实现元素倒序，并返回栈B的栈顶元素

时间复杂度：appenTail()为O(1);deleteHead()在N次队首元素删除操作中总共需完成N个元素的倒序。

空间复杂度：最差情况下，栈A和栈B共保存N个元素

class CQueue {
public:
    stack<int> A,B;
    CQueue() {
        
    }
    
    void appendTail(int value) {
        A.push(value);
    }
    
    int deleteHead() {
        //栈B不空
        if(!B.empty()){
            int res = B.top();
            B.pop();
            return res;
        }
        //B空A空
        if(A.empty()){
            return -1;
        }
        //B空A不空，将A中元素倒序到B中
        while(!A.empty()){
            B.push(A.top());
            A.pop();
        }
        int ans = B.top();
        B.pop();
        return ans;
    }
};

####10- I. 斐波那契数列

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例：

输入：n=2

输出：1

思路：

方法一：递归法

原理：把f(n)问题拆分为f(n-1)和f(n-2)两个子问题的计算，以f(0),f(1)为终止条件。

缺点：大量重复的递归计算

class Solution {
public:
    int fib(int n) {
        if(n==0) return 0;
        if(n==1 || n==2) return 1;
        return (fib(n-1)+fib(n-2))%1000000007; 
    }
};

方法二：记忆化递归

原理：在递归法的基础上，新建一个长度为n的数组，用于递归时存储f(0)至f(n)的数字值，重复遇到某数字时则直接从数组取用，避免重复的递归计算。

缺点：需要使用O(N)的额外空间。

方法三：动态规划

原理：以斐波那契数列性质f(n+1)=f(n)+f(n-1)为转移方程。

动态规划解析：

状态定义：设dp为一维数组，其中dp[i]的值代表斐波那契数列第几个数字。
转移方程：dp[i+1] = dp[i] + dp[i-1]
初始状态：dp[0]=0,dp[1]=1
返回值：dp[n],即斐波那契数列的第n个数字

空间复杂度分析：

若新建长度为 n 的 dp 列表，则空间复杂度为 O(N) 。

由于dp列表第i项只与第i-1和第i-2有关，因此只需要初始化三个整形变量sum、a、b，利用辅助sum使a,b两数字交替前进即可。
节省了dp列表空间，因此空间复杂度降至O(1)。

class Solution {
public:
    int fib(int n) {
        if(n==0 || n==1) return n;
        int a = 0,b=1,sum=a+b;
        for(int i=2;i<n;i++){
            a = b;
            b =sum;
            sum = (a+b)%1000000007;
        }
        return sum;
    }
};

10- II. 青蛙跳台阶问题

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例：

输入：n=2

输出：2

输入：n=7

输出：21

输入：n=0

输出：0

思路：

也是斐波那契数列的变形，到达第n阶，则前面一定是n-1或者n-2,也就是f(n)=f(n-1)+f(n-2)

方法一：时间复杂度为O(n)，空间复杂度为O(n)

class Solution {
public:
    int numWays(int n) {
        if(n==0 || n==1) return 1;
        int dp[n+1];
        dp[1]=1;
        dp[2]=2;
        for(int i=3;i<=n;i++){
            dp[i] = (dp[i-1]+dp[i-2])%1000000007;
        }
        return dp[n];
    }
};

复杂度为O(1)

class Solution {
public:
    int numWays(int n) {
        if(n==0 || n==1) return 1;
        int a=1,b=2,sum;
        for(int i=3;i<=n;i++){
            sum = (a+b)%1000000007;
            a=b;
            b=sum;
        }
        return b;
    }
};

11. 旋转数组的最小数字

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

给你一个可能存在重复元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为1。

示例：

输入：[3,4,5,1,2]

输出：1

思路：

方法一：排序直接输出

class Solution {
public:
    int minArray(vector<int>& numbers) {
        if(numbers.size()<=0) return 0;
        sort(numbers.begin(),numbers.end());
        return numbers[0];
    }
};

方法二：二分查找

算法流程：

1，初始化：声明i,j双指针分别指向nums数组左右两端

2，循环二分：设m=(i+j)/2为每次二分的中点，可分为以下三种情况：

当nums[m] > nums[j]时：m一定在左排序数组中，即旋转点x一定在[m+1,j]，因此执行i=m+1;
当nums[m] < nums[j]时：m一定在右排序数组中，即旋转点x一定在[i,m]，因此执行j=m;
当nums[m] = nums[j]时：无法判断m在哪个排序数组中，即无法判断旋转点x在[i,m]还是[m+1,j]中。解决方案：直接遍历

3，返回值：当j=j时跳出循环，并返回旋转点的值nums[i]即可。

class Solution {
public:
    int minArray(vector<int>& numbers) {
        int i=0,j=numbers.size()-1;
        while(i<j){
            int m=(i+j)/2;
            if(numbers[m]>numbers[j]) i=m+1;
            else if(numbers[m]<numbers[j]) j=m;
            else{
                int x =i;
                for(int k=i+1;k<j;k++){
                    if(numbers[k]<numbers[x]) x=k;
                }
                return numbers[x];
            }
        }
        return numbers[i];
    }
};

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例：

输入：m=2,n=3,k=1

输出：3

输入：m=3,n=1,k=0

输出：0

思路：

方法一：深度优先遍历DFS

DFS通过递归，先朝一个方向搜到底，再回溯至上一个节点，沿另一个方向搜索。

剪枝：在搜索中，遇到数位和超出目标值、此元素已访问，则应立即返回，称之为可行性剪枝。

算法解析：

递归参数： 当前元素在矩阵中的行列索引i和j,两者的数位和si,sj;

终止条件： 当行列索引越界或数位和超出目标值K或当前元素已经访问过，返回0，代表计入不可达;

递推工作：

1，标记当前单元格：将索引(i,j)存入set visited中，代表此单元格已经访问过。

2，搜索下一单元格：计算当前元素的下，右两个方向元素的数位和，并开启下层递归。

回溯返回值： 返回 1 + 右边搜索可达解总数 + 下边可达解总数，代表从本单元格递归搜索的可达解总数;

代码1：

class Solution {
public:
    int movingCount(int m, int n, int k) {
        //标记数组
        vector<vector<bool> > visited(m,vector<bool>(n,0));
        //递归访问
        return dfs(visited,m,n,k,0,0);
    }
private:
    int dfs(vector<vector<bool> >& visited,int m,int n,int k,int i, int j){
        //递归终止条件
        if(i>=m || j>=n || visited[i][j] || bitSum(i)+bitSum(j) > k) return 0;
        //访问
        visited[i][j]=1;
        //递归访问下边和右边
        return 1 + dfs(visited,m,n,k,i+1,j) + dfs(visited,m,n,k,i,j+1);
    }
    
    //计算数位和
    int bitSum(int n){
        int sum = 0;
        while(n>0){
            sum += n % 10;
            n /= 10;
        }
        return sum;
    }
};

方法二：广度优先遍历BFS

BFS通常利用队列实现

算法解析：

初始化: 将机器人初始点(0,0)加入队列queue

递归终止条件： queue为空。代表已遍历完所有可达解；

迭代工作：

1，单元格出队：将队首单元格的索引，数位和弹出，作为当前搜索单元格；

2，判断是否跳过：当行列索引越界或数位和超出目标值K或当前元素已经访问过，返回0，代表计入不可达，执行continue;

3，标记当前单元格：将单元格索引(i,j)存入visited中，代表此单元格已被访问过；

4，单元格入队：将当前元素的下边、右边单元格的索引、数位和加入queue中；

返回值： visited的长度即为可达解数量;

代码2:

class Solution {
public:
    int movingCount(int m, int n, int k) {
        //标记数组
        vector<vector<bool> > visited(m,vector<bool>(n,0));
        int res = 0;
        //辅助队列
        queue<vector<int> > que;
        que.push({0,0,0,0});
        while(que.size()>0){
            //弹出队首元素
            vector<int> x = que.front();
            que.pop();
            int i=x[0],j=x[1],si=x[2],sj=x[3];
            if(i>=m || j>=n || visited[i][j] || si + sj > k) continue;
            //访问
            visited[i][j] = true;
            res++;
            //将下边和右边入队
            que.push({i+1,j,bitSum(i+1),sj});
            que.push({i,j+1,si,bitSum(j+1)});
        }
        return res;
    }
private:
int bitSum(int n){
        int sum = 0;
        while(n>0){
            sum += n % 10;
            n /= 10;
        }
        return sum;
    }
};

14- I. 剪绳子

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

示例：

输入：2

输出：1

思路：

关于为什么切分为3的优先级最高可以利用均值不等式求出乘积最大值 L(m)=(n/m)^m 对此式求导（可利用对数法），

可以证明当 m=n/e 时，乘积取最大，此时每段绳子的长度为 n/(n/e)=e，自然对数e的值为2.718，显然接近3，所以总体来讲3最好

均值不等式

\[ \frac{n_1+n_2+...n_a}n \quad \geq \sqrt[n]{n_1n_2...n_a} \]

由数学推导可得：

1，当所有绳段长度相等时，乘积最大。

2，最优的绳段长度为3

切分规则：

1，最优：3.把绳子尽可能切为多个长度为3的片段，留下的最后一段绳子的长度可能为9，1，2三种情况

2，次优：2.若最后一段绳子长度为2；则保留，不再拆分为1+1

3，最差：1，若最后一段绳子长度为1；则应把一份3+1替换成2+2。

算法流程：

1，当n<=3时，按照规则应不切分，但由于题目要求必须切成m>1段，因此必须剪出一段长度为1的绳子，即返回n-1

2，当n>3时，求n除以3的整数部分a和余数部分b(即n=3a+b)，并分为以下三种情况：

当b=0时，直接返回3^n

当b=1时，要将一个1+3转换为2+2,因此返回3^(a-1)*4

当b=2时，返回3^a*2

时间复杂度：O(1)

空间复杂度：O(1)

class Solution {
public:
    int cuttingRope(int n) {
        if(n<=3) return n-1;
        int a = n/3,b = n%3;
        if(b==0) return pow(3,a);
        if(b==1) return pow(3,a-1)*4;
        else return pow(3,a)*2;
    }
};

方法二：动态规划:

class Solution {
public:
    int cuttingRope(int n) {
        if(n<=3) return n-1;
        //里的3可以不需要再分了，因为3分段最大才2，不分就是3。记录最大的。
        int dp[n+1];
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 3;
        for(int i=4;i<=n;i++){
            int maxValue = 0;
            for(int j=1;j<=i/2;j++){
                maxValue = max(maxValue,dp[j]*dp[i-j]);
            }
            dp[i] = maxValue;
        }
        return dp[n];
    }
};

14- II. 剪绳子 II

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m - 1] 。请问 k[0]*k[1]*...*k[m - 1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

在上一题的基础上取模,最佳方法就是快速幂

class Solution {
public:
    int cuttingRope(int n) {
        if(n<=3) return n-1;
        int a = n/3,b=n%3,k= 1000000007;
        if(b==0) return quick_mod(3,a,k)%k;
        if(b==1) return quick_mod(3,a-1,k)*4%k;
        else return quick_mod(3,a,k)*2%k;
    }
private:
    //快速幂
    long long quick_mod(long x,long y,long k){
        long long ans = 1;
        //对刚进来的x进行取模运算，避免后面第一次求平方溢出
        x %= k;
        while(y){
            if(y&1){
                ans = ans*x%k;
            }
            y>>=1;
            x = x * x %k;
        }
        return ans%k;
    }
};

方法二：循环求余

class Solution {
   public int cuttingRope(int n) {
        if(n <= 3) return n - 1;
        int b = n % 3, p = 1000000007;

        long rem = 1, x = 3 ,a = n / 3;
        //直接套循环求余公式
        for(int i = 0; i < ((b == 1)?a-1:a); i++) { //b == 1代表余数为1的时候，需要单独取出一个3出来凑成2*2达到最大值效果
            rem = (rem * x) % p;
        }  
        if(b == 0) return (int)(rem % p);
        if(b == 1) return (int)(rem * 4 % p);
        return (int)(rem * 2 % p);
    }
};

15. 二进制中1的个数

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 '1' 的个数（也被称为汉明重量).）。

提示：

请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在上面的示例 3 中，输入表示有符号整数 -3。

示例：

输入：n = 11 (控制台输入 00000000000000000000000000001011)
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 '1'。

思路：

方法一:

&1,并且右移1位

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int count = 0;
        while(n){
            if(n&1){
                count++;
            }
            n>>=1;
        }
        return count;
    }
};

方法二：

直接n&(n-1)即可得到1的数量

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int count = 0;
        while(n){
            n &= n-1;
            count++;
        }
        return count;
    }
};

16. 数值的整数次方

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn）。不得使用库函数，同时不需要考虑大数问题

示例：

输入：x = 2.00000, n = 10
输出：1024.00000

输入：x = 2.10000, n = 3
输出：9.26100

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

思路：

快速幂，但是需要注意当n = (-1)*n时会出现错误，我们需要把n放到long中

class Solution {
public:
    double myPow(double x, int n) {
        double sum;
        long m = n;
        if(n==0 || x==1) return 1;
        if(n>0){
            sum = quick_mod(x,m);
        }
        else{
            m = (-1)*m;
            sum = 1/quick_mod(x,m);
        }
        return sum;
    }
private:
    double quick_mod(double x,long y){
        double ans = 1;
        while(y){
            if(y&1){
                ans = ans*x;
            }
            y>>=1;
            x = x*x;
        }
        return ans;
    }
};

17. 打印从1到最大的n位数

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

示例：

输入: n = 1 输出: [1,2,3,4,5,6,7,8,9]

思路：

不考虑大数的话

class Solution {
public:
    vector<int> printNumbers(int n) {
        int high = pow(10,n)-1;
        vector<int> res(high);
        for(int i=0;i<high;i++){
            res[i]=i+1;
        }
        return res;
    }
};

考虑大数

我们要转化为string来处理

递归生成全排列:

基于分治算法的思想，先固定高位，向低位递归，当个位已被固定时，添加数字的字符串。例如当n=2时，(数字范围1-99)，固定十位为0-9，按顺序依次开启递归，固定个位0-9，终止递归并添加数字字符串。

但是也有两个问题

1，删除高位多余的0

2，列表从1开始

class Solution {
public:
    vector<string> res;
    string cur;
    char num[10] = {'0','1','2','3','4','5','6','7','8','9'};
    vector<string> printNumbers(int n) {
        //数字长度
        for(int i=1;i<=n;i++) dfs(0,i);
        return res;
    }
    void dfs(int x,int len){
      	//添加到结果中
        if(x==len){
            res.push_back(cur);
            return;
        }
        //x=0表示左边第一位数字，不能为0
        int start = x==0 ? 1 : 0;
        for(int i=start;i<10;i++){
            //确定本位数字
            cur.push_back(num[i]);
            //确定下一位数字
            dfs(x+1,len);
            //删除本位数字
            cur.pop_back();
        }
    }
};

转化为int

class Solution {
public:
    vector<string> res;
    string cur;
    char num[10] = {'0','1','2','3','4','5','6','7','8','9'};
    vector<int> printNumbers(int n) {
        //数字长度
        for(int i=1;i<=n;i++) dfs(0,i);
        vector<int> res_int;
        for(int i=0;i<res.size();i++){
            res_int.push_back(stoi(res[i]));
        }
        return res_int;
    }
    void dfs(int x,int len){
        if(x==len){
            res.push_back(cur);
            return;
        }
        //x=0表示左边第一位数字，不能为0
        int start = x==0 ? 1 : 0;
        for(int i=start;i<10;i++){
            //确定本位数字
            cur.push_back(num[i]);
            //确定下一位数字
            dfs(x+1,len);
            //删除本位数字
            cur.pop_back();
        }
    }
};

18. 删除链表的节点

给定单向链表的头指针和一个要删除的节点的值，定义一个函数删除该节点。

返回删除后的链表的头节点。

注意：此题对比原题有改动

示例：

输入: head = [4,5,1,9], val = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9.

思路：

双指针法：

算法流程：

1，定义*pre = head*· *cur=head->next*

2，判断当cur不为空和cur->val != val 时，指针向前运动

3，返回值：如果cur不为空，代表找到了，我们只需要删除即可，最后返回头节点

class Solution {
public:
    ListNode* deleteNode(ListNode* head, int val) {
        if(head==nullptr) return head;
        if(head->val==val) return head->next;
        ListNode* cur = head->next,*pre=head;
        while(cur!=nullptr && cur->val != val){
            pre = cur;
            cur = cur->next;
        }
        if(cur != nullptr) pre->next = cur->next;
        return head;
    }
};

21. 调整数组顺序使奇数位于偶数前面

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有奇数在数组的前半部分，所有偶数在数组的后半部分。

示例：

输入：

nums=[1,2,3,4]

输出：

[1,3,2,4]或[3,1,2,4]

思路：

排序

方法一：采用双指针法

定义双指针在数组两端，循环执行（i=j时跳出）：

1，指针i从左往右寻找偶数

2，指针j从右往左寻找奇数

3，交换

class Solution {
public:
    vector<int> exchange(vector<int>& nums) {
        int i = 0,j = nums.size()-1;
        while(i<j){
            while(i<j && (nums[i] & 1) == 1) i++;
            while(i<j && (nums[j] & 1) == 0) j--;
            swap(nums[i],nums[j]);
        }
        return nums;
    }
};

方法二：快慢指针

class Solution {
public:
    vector<int> exchange(vector<int>& nums) {
        int slow =0,fast=0;
        while(fast<nums.size()){
            if(nums[fast]&1){
                swap(nums[slow],nums[fast]);
                slow++;
            }
            fast++;
        }
        return nums;
    }
};

22. 链表中倒数第k个节点

输入一个链表，输出该链表中倒数第k个节点。为了符合大多数人的习惯，本题从1开始计数，即链表的尾节点是倒数第1个节点。

例如，一个链表有 6 个节点，从头节点开始，它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。

示例：

给定一个链表: 1->2->3->4->5, 和 k = 2.

返回链表 4->5.

思路：

方法一：

1，先遍历求链表长度n

2，再回到头节点走n-k步

class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        int n = 0;
        ListNode *cur = head;
        //确定链表长度
        while(cur!=nullptr){
            n++;
            cur = cur->next;
        }
        //判断溢出
        if(k>n) return nullptr;
        //回到头节点
        cur = head;
        //移动到第n-k个位置
        for(int i=0;i<n-k;i++){
            cur = cur->next;
        }
        return cur;
    }
};

方法二：双指针

1，定义一个指针cur向前走k步，pre指向头节点

2，判断溢出

3，两个指针同时运动，直到cur指向null,返回pre

class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        ListNode *pre = head,*cur=head;
        for(int i=0;i<k;i++){
            //判断溢出
            if(cur==nullptr) return nullptr;
            cur = cur->next;
        }
        while(cur!=nullptr){
            cur = cur->next;
            pre = pre ->next;
        }
        return pre;
    }
};

24. 反转链表

定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

示例：

输入：1->2->3->4->5->NULL

输出：5->4->3->2->1->NULL

思路：

方法一：双指针

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* cur = head,*pre=nullptr;
        while(cur!=nullptr){
            ListNode* tmp = cur->next;
            cur->next = pre;
            pre = cur;
            cur = tmp;
        }
        return pre;
    }
};

方法二：递归

算法流程：

recur(cur,pre):

1，终止条件：当cur为空，则返回尾节点pre(即反转链表的头节点)

2，递归后继节点，记录返回值为res

3，修改当前节点cur指向前驱节点pre

4，返回res

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        return recur(head,nullptr);
    }
private:
    ListNode* recur(ListNode* cur,ListNode* pre){
        //终止条件
        if(cur==nullptr) return pre;
        //递归后继节点
        ListNode* res = recur(cur->next,cur);
        //修改节点引用指向
        cur->next = pre;
        return res;
    }
};

25. 合并两个排序的链表

输入两个递增排序的链表，合并这两个链表并使新链表中的节点仍然是递增排序的。

示例：

输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

思路：

方法一：双指针

双指针l1、l2遍历两链表。

算法流程：

1，初始化：创建伪节点dum,节点cur指向dum

2，循环合并：当l1或l2为空时跳出：

当l1.val < l2.val时：cur的后继节点指定为l1,l1向前走一步
当l1.val >= l2.val时：cur的后继节点指定为l2,l2向前走一步
节点cur向前走一步，即cur=cur->next

3，合并剩余尾部

l1不空，将l1添加至节点cur后
否则，将l2添加至节点cur之后

4，返回值：合并链表在伪节点dum之后，因此返回dum->next

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        //判断
        if(l1==nullptr) return l2;
        if(l2==nullptr) return l1;
        if(l1==nullptr && l2==nullptr) return nullptr;
        //创建伪节点
        ListNode* dum = new ListNode(0),*cur = dum;
        //循环合并
        while(l1 != nullptr && l2 != nullptr){
            //l1->val<l2.val，指向l1
            if(l1->val < l2->val){
                cur->next = l1;
                l1 = l1->next;
            }else{
                cur->next = l2;
                l2 = l2->next;
            }
            cur = cur->next;
        }
        //合并剩余尾部
        cur->next = l1 != nullptr ? l1 : l2;
        return dum->next;
    }
};

方法二：递归

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        //判断
        if(l1==nullptr) return l2;
        if(l2==nullptr) return l1;
        if(l1==nullptr && l2==nullptr) return nullptr;
        
        if(l1->val <= l2->val){
            l1->next = mergeTwoLists(l1->next,l2);
            return l1;
        }else{
            l2->next = mergeTwoLists(l1,l2->next);
            return l2;
        }
    }
};

27. 二叉树的镜像

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

例如输入：

4 /
2 7 / /
1 3 6 9

镜像输出：

4 /
7 2 / /
9 6 3 1

示例：

输入：root = [4,2,7,1,3,6,9] 输出：[4,7,2,9,6,3,1]

思路：

方法一：递归

根据二叉树镜像的定义，考虑递归(dfs)二叉树，交换每个节点的左/右子节点，即可生成二叉树的镜像

算法流程：

1，终止条件：当root为空时，返回null

2，递推工作：

初始化节点tmp,用于暂存root的左子节点；
开启递归右子节点mirrorTree(root->right)，并将返回值作为root的左子节点；
开启递归右子节点mirrorTree(tmp)，并将返回值作为root的右子节点；

3，返回值：返回当前节点root

class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if(root==nullptr) return nullptr;
        TreeNode* tmp = root->left;
        root->left = mirrorTree(root->right);
        root->right = mirrorTree(tmp);
        return root;
    }
};

方法二：辅助栈

算法流程：

1，初始化：设置一个链表栈，root入栈

2，设置node指针指向栈顶，然后出栈，左右子树入栈

3，交换左右子树

4，返回root

class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if(root==nullptr) return nullptr;
        stack<TreeNode*> st;
        st.push(root);
        while(!st.empty()){
            TreeNode* node = st.top();
            //出栈
            st.pop();
            //左右子树入栈
            if(node->left != nullptr) st.push(node->left);
            if(node->right != nullptr) st.push(node->right);
            //交换左右子树
            TreeNode* tmp = node->left;
            node->left = node->right;
            node->right = tmp;
        }
        return root;
    }
};

28. 对称的二叉树

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

1 /
2 2 / /
3 4 4 3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

1 /
2 2
3 3

示例：

输入：root = [1,2,2,3,4,4,3] 输出：true

思路：

对称二叉树定义：对于树中任意两个对称节点L和R，一定有：

1，L.val = R.val

2，L.left.val = R.right.val

3，L.right.val = R.left.val

算法流程：

1，终止条件：

当L和R同时越过叶节点；此树丛顶至顶都对称，返回true
当L或R中有一个越过叶节点：此树不对称，返回false
当节点L值 != R值：不对称，返回false

2，递推工作：

判断两节点L.left和R.right是否对称,即recur(L.left,R.right);
判断两节点L.right和R.left是否对称,即recur(L.right,R.left);

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(root == nullptr) return true;
        //递归
        return recur(root->left,root->right);
    }
    bool recur(TreeNode* L,TreeNode* R){
        //左右同时结束
        if(L==nullptr && R==nullptr) return true;
        //左子树或者右子树一边没有元素或者两边不等
        if(L == nullptr || R==nullptr || L->val != R->val) return false;
        //递归
        return recur(L->left,R->right) && recur(L->right,R->left);
    }
};

30. 包含min函数的栈

定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

示例：

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.min(); --> 返回 -2.

思路：

普通栈push()和pop()复杂度为O(1),而获取栈最小值min()需要遍历整个栈，复杂度为O(N);

我们可以通过建立辅助栈实现：

数据栈A：栈A用于存储所有元素，保证push()、pop()、top()函数的正常逻辑
数据栈B：栈B中存储栈A中所有非严格降序的元素，则栈A中的最小元素始终对应栈B的栈顶元素，即min()只需返回栈B的栈顶元素即可；

#####算法流程：

push(x): 重点保持栈B的元素是非严格降序的

1，将x压入栈A；

2，若栈B为空或x小于等于栈B的栈顶元素，则将x压入栈B

pop():重点保持栈A，B的元素一致性

1，执行栈A出栈，将出栈元素记为y;

2，若y等于栈B的栈顶元素，则执行栈B出栈；

top():直接返回栈A的栈顶元素

min():直接返回栈B的栈顶元素

class MinStack {
public:
    /** initialize your data structure here. */
    stack<int>A,B;
    MinStack() {

    }
    
    void push(int x) {
        A.push(x);
        //B空或者栈B的栈顶元素小于x，入栈B
        if(B.empty() || x<=B.top()){
            B.push(x);
        }
    }
    
    void pop() {
        int y=A.top();
        A.pop();
        //保持一致性
        if(B.top()==y){
            B.pop();
        }
    }
    
    int top() {
        return A.top();
    }
    
    int min() {
        return B.top();
    }
};

35. 复杂链表的复制

请实现 copyRandomList 函数，复制一个复杂链表。在复杂链表中，每个节点除了有一个 next 指针指向下一个节点，还有一个 random 指针指向链表中的任意节点或者 null。

示例1: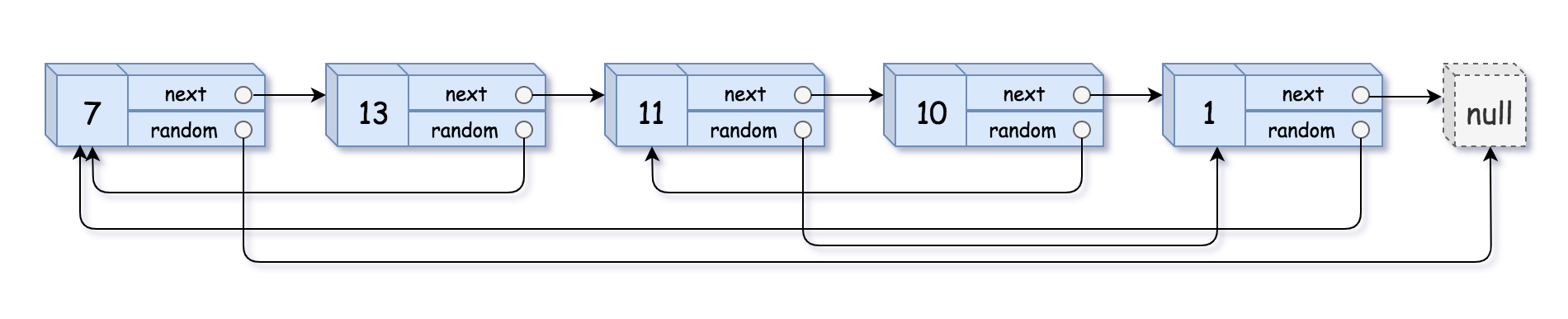

输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]

输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

思路：

方法一：哈希表

利用哈希表的查询特点，考虑构建原链表节点和新链表对应节点的键值对映射关系，

再遍历构建新链表各节点的 next 和 random 引用指向即可。

算法流程：

1，若头节点head为空节点，直接返回null;

2，初始化：哈希表dic，节点cur指向头节点;

3，复制链表：

建立新节点，并向dic添加键值对(原cur节点，新cur节点)
cur遍历至原链表下一节点；

4，构建新链表的引用指向：

1，构建新节点的next和random引用指向；
2，cur遍历至原链表下一节点；

5，返回值：新链表的头节点dic[cur]；

时间复杂度O(N): 两轮遍历链表，使用O(N)时间。

空间复杂度O(N)：哈希表dic使用线性大小的额外空间；

class Solution {
public:
    Node* copyRandomList(Node* head) {
        if(head==nullptr) return nullptr;
        Node* cur = head;
        unordered_map<Node*,Node*>map;
        //复制链表，并建立“原节点->新节点“的map映射
        while(cur != nullptr){
            map[cur] = new Node(cur->val);
            cur = cur->next;
        }
        //指向头节点,重新遍历
        cur = head;
        //构建新链表的next和random指向
        while(cur != nullptr){
            map[cur]->next = map[cur->next];
            map[cur]->random = map[cur->random];
            cur = cur->next;
        }
        //返回新链表的头节点
        return map[head];
    }
};

方法二：拼接+拆分

考虑构建: 原节点1->新节点1->原节点2->新节点2->....的拼接链表，如此便可在访问原节点的random指向节点

的同时找到新对应新节点的random指向节点;

算法流程：

1，复制各节点，构建拼接链表：

设原节点为node1->node2...,构建成node1->node1->node2->node2->....

2，构建新链表各节点的random指向：

当访问原节点cur的随机指向节点cur.random时，对应新节点的cur.next的随机指向节点为cur.random->next

3，拆分原/新链表：

设置pre/cur分别指向原/新链表头节点，遍历执行pre.next = pre.next.next和cur.next = cur.next.next将两链表拆分开

4，返回新链表的头节点res即可

class Solution {
public:
    Node* copyRandomList(Node* head) {
        if(head == nullptr) return nullptr;
        //设置cur指向头节点
        Node* cur = head;
        //1，复制各节点，并构建拼接新链表
        while(cur != nullptr){
            //构建新节点
            Node* tmp = new Node(cur->val);
            tmp->next = cur->next;
            cur->next = tmp;
            cur = tmp->next;
        }
        //构建各新节点的random指向
        //返回头节点，重新遍历
        cur = head;
        while(cur != nullptr){
            if(cur->random != nullptr){
                cur->next->random = cur->random->next;
            }
            cur = cur->next->next;
        }
        //3,拆分两链表
        cur=head->next;
        Node* pre = head,*res = head->next;
        while(cur->next != nullptr){
            pre->next = pre->next->next;
            cur->next = cur->next->next;
            pre = pre->next;
            cur = cur->next;
        }
        //单独处理原链表尾节点
        pre->next = nullptr;
        return res;
    }
};

39. 数组中出现次数超过一半的数字

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例：

输入：

[1,2,3,2,2,2,5,4,2]

输出：

2

思路：

方法一：哈希表统计法

时间空间复杂度为O(N)

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        map<int,int>mp;
        for(auto num:nums){
            mp[num]++;
            if(mp[num] > (nums.size()/2)){
                return num;
            }
        }
        return 0;
    }
};

方法二：数组排序法

将数组排序，数组中点的元素一定为众数

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        return nums[nums.size()/2];
    }
};

方法三：摩尔投票法

投票法简单来说就是不同则抵消，占半数以上的数字必然留到最后。这句话是摩尔投票法的精髓

时间和空间复杂度为O(N)和O(1)

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int x=0,votes=0,count=0;
        for(int num:nums){
            if(votes==0) x=num;
            votes += num == x ? 1:-1;
        }
        //验收
        for(int num:nums)
            if(num == x) count++;
        return count>nums.size()/2 ? x:0;
    }
};

40. 最小的k个数

输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

示例：

输入：arr = [3,2,1], k = 2

输出：[1,2] 或者 [2,1]

输入：arr = [0,1,2,1],k = 1

输出：[0]

ToK问题：

方法一：快排

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        vector<int> vec(k,0);
        sort(arr.begin(),arr.end());
        for(int i=0;i<k;i++){
            vec[i]=arr[i];
        }
        return vec;
    }
};

不用api

快速排序原理：

快速排序算法有两个核心点，分别为 “哨兵划分” 和 “递归” 。

哨兵划分操作：以数组某个元素（一般选取首元素）为基准数，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        quickSort(arr,0,arr.size()-1);
        vector<int>res;
        //assign()函数主要是将一个容器中元素全部复制到另一个容器中
        res.assign(arr.begin(),arr.begin()+k);
        return res;
    }
private:
    void quickSort(vector<int>& arr, int l, int r){
        //子数组长度为1时递归终止
        if(l>=r) return;
        //哨兵划分操作（以arr[1]作为基准）
        int i=l,j=r;
        while(i<j){
            while(i<j && arr[j]>=arr[l]) j--;
            while(i<j && arr[i]<=arr[l]) i++;
            swap(arr[i],arr[j]);
        }
        //使左边小于等于基准，右边大于等于基准
        swap(arr[i],arr[l]);
        //递归左右子数组执行哨兵划分
        quickSort(arr,l,i-1);
        quickSort(arr,i+1,r);
    }
};

方法二：基于快速排序的数组划分

题目只要求返回最小的 k 个数，对这 k 个数的顺序并没有要求。因此，只需要将数组划分为最小的 k 个数和其他数字两部分即可，而快速排序的哨兵划分可完成此目标。

根据快速排序原理，如果某次哨兵划分后基准数正好是第 k+1 小的数字，那么此时基准数左边的所有数字便是题目所求的最小的 k 个数。

根据此思路，考虑在每次哨兵划分后，判断基准数在数组中的索引是否等于k ，若 true 则直接返回此时数组的前k 个数字即可。

算法流程：

getLeastNumbers()

1，若k大于数组长度，则直接返回整个数组；

2，执行并返回quick_sort()

quick_sort()

功能不是排序整个数组，而是搜索并返回最小的k个数

哨兵划分：

划分完毕后，基准数为arr[i],左/右子数组区间分别为[l,i-1],[i+1,r];

递归或返回：
- 若K < i，代表第 k+1 小的数字在左子数组中，则递归左子数组；
- 若K > i，代表第 k+1 小的数字在右子数组中，则递归右子数组；
- 若K = i，代表此时arr[k]即为第k+1小的数字，则直接返回数组前k个数字即可；

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        if(k>=arr.size()) return arr;
        return quick_sort(arr,k,0,arr.size()-1);
    }
private:
    vector<int> quick_sort(vector<int>& arr,int k,int l,int r){
        int i=l,j=r;
        while(i<j){
            while(i<j && arr[j] >= arr[l]) j--;
            while(i<j && arr[i] <= arr[l]) i++;
            swap(arr[i],arr[j]);
        }
        swap(arr[i],arr[l]);
        //递归左数组
        if(i>k) return quick_sort(arr,k,l,i-1);
        //递归右数组
        if(i<k) return quick_sort(arr,k,i+1,r);
        vector<int>res;
        res.assign(arr.begin(),arr.begin()+k);
        return res;
    }
};

方法三：堆

我们用一个大根堆实时维护数组的前 k 小值。首先将前k个数插入大根堆中，

随后从第k+1 个数开始遍历，如果当前遍历到的数比大根堆的堆顶的数要小，就把堆顶的数弹出，再插入当前遍历到的数。

最后将大根堆里的数存入数组返回即可。在下面的代码中，由于 C++ 语言中的堆（即优先队列）为大根堆，我们可以这么做。

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        vector<int> vec(k,0);
        if(k==0) return vec;
        priority_queue<int> Q;
        //把前k个数入堆
        for(int i=0;i<k;i++){
            Q.push(arr[i]);
        }
        for(int i=k;i<arr.size();i++){
            //把堆中大的元素出堆
            if(Q.top()>arr[i]){
                Q.pop();
                Q.push(arr[i]);
            }
        }
        //输出堆中的元素即最小k位
        for(int i=0;i<k;i++){
            vec[i]=Q.top();
            Q.pop();
        }
        return vec;
    }
};

41. 数据流中的中位数

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

例如，

[2,3,4] 的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

void addNum(int num) - 从数据流中添加一个整数到数据结构中。 double findMedian() - 返回目前所有元素的中位数。

示例：

输入：

["MedianFinder","addNum","addNum","findMedian","addNum","findMedian"]

[[],[1],[2],[],[3],[]]

输出：

[null,null,null,1.50000,null,2.00000]

方法：用大小堆

小顶堆A保存较大的数

大顶堆B保存较小的数

A和B尽量保存一样的数量，中位数可以根据栈顶元素计算得出

算法流程：

设元素总数为N=m+n,m和n分别为A和B中的元素

addNum(num)函数

1，当m=n(即N为偶数时)：需向A添加一个元素。实现方法：将新元素num插入至B，再将B堆顶元素插入至A；

2，当m≠n(即N为奇数时)：需向B添加一个元素。实现方法：将新元素num插入至A，再将A堆顶元素插入至B；

这样始终保持A保存较大一半、B保存较小一半。

findMedian()函数

1，当m=n：中位数为(A的堆顶元素+B的堆顶元素)/2；

2，当m≠n(即N为奇数时)：则中位数为A的堆顶元素

class MedianFinder {
public:
    // 最大堆，存储左边一半的数据，堆顶为最大值
    priority_queue<int,vector<int>,less<int>> maxHeap_B;
    // 最小堆， 存储右边一半的数据，堆顶为最小值
    priority_queue<int,vector<int>,greater<int>> minHeap_A;
    /** initialize your data structure here. */
    MedianFinder() {

    }
    
    // 维持堆数据平衡，并保证左边堆的最大值小于或等于右边堆的最小值
    void addNum(int num) {
        //当m=n(即N为偶数时)：需向A添加一个元素。实现方法：将新元素num插入至B，再将B堆顶元素插入至A；
        if(maxHeap_B.size()==minHeap_A.size()){
            maxHeap_B.push(num);
            int top=maxHeap_B.top();
            maxHeap_B.pop();
            minHeap_A.push(top);
        }else{
            minHeap_A.push(num);
            int top=minHeap_A.top();
            minHeap_A.pop();
            maxHeap_B.push(top);
        }
    }
    
    double findMedian() {
        if(minHeap_A.size()==maxHeap_B.size()){
            return (maxHeap_B.top()+minHeap_A.top())*1.0/2;
        }else{
            return minHeap_A.top()*1.0;
        }
    }
};

44. 数字序列中某一位的数字

数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中，第5位（从下标0开始计数）是5，第13位是1，第19位是4，等等。

请写一个函数，求任意第n位对应的数字。

示例：

输入：n = 3

输出：3

输入：n = 11

输出：0

思路：

数字范围	位数	数字数量	数位数量
1-9	1	9	9
10-99	2	90	180
100-999	3	900	2700
...	...	...	...
start - end	digit	9*start	9startdigit

1，确定n所在数字的位数，记为digit;

2，确定n所在的数字，记为num;

3，确定n是num中的哪一数位，并返回结果;

class Solution {
public:
    int findNthDigit(int n) {
        //数位
        int digit = 1;
        //当前数字范围的左区间
        long start = 1;
        //数位数量
        long count = 9;

        //定位目标数字所在的数字范围
        while(n>count){
            n -= count;
            digit += 1;
            start *= 10;
            count = 9*start*digit;
        }
        //确定n所在的数字
        long num = start + (n-1) / digit;
        //index最大取digit-1，即此时num坐标从左往右为0,1...digit-1,共digit位
        int index = (n-1)%digit;
        while(index<(digit-1)){
            //最后的结果是num中的第index个数字
            num/=10;
            digit--;
        }
        //结果为num右侧末尾数字
        return num%10;
    }
};

51. 数组中的逆序对

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例：

输入：[7,5,6,4]

输出：5

思路：

归并排序与逆序对是息息相关的归并排序体现了“分治思想”

算法流程：

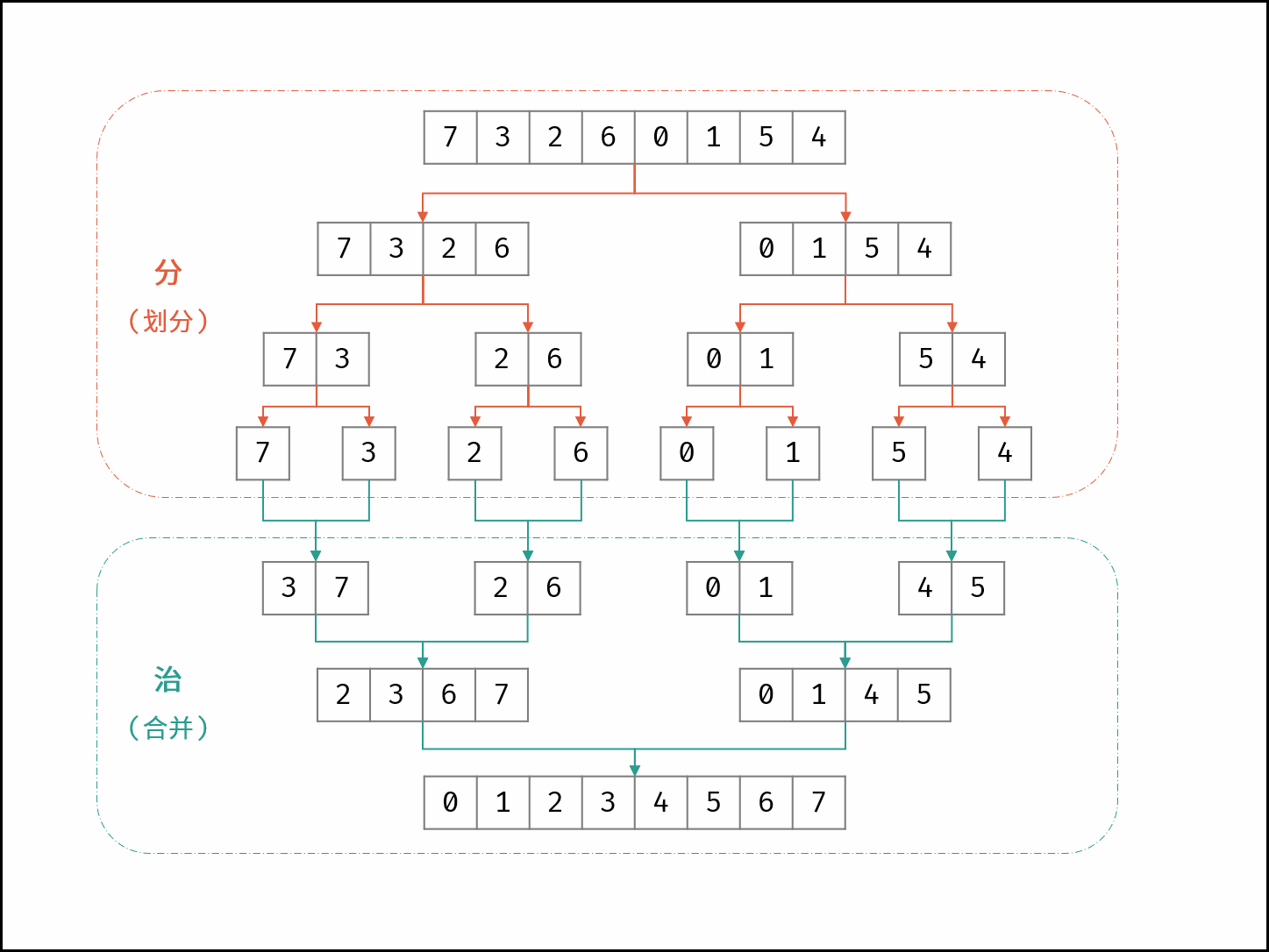
merge_sort()归并排序与逆序对统计：

1，终止条件： 当l>=r时，代表子数组长度为1，此时终止划分；

2，递归划分： 计算数组中点m，递归划分左子数组merge_sort(1,m)和右子数组merge_sort(m+1,r);

3，合并与逆序对统计：

（1），暂存数组nums[i,r]内的元素至辅助数组tmp；

（2），循环合并：设置双指针i,j分别指向左/右子数组的首元素：

当i=m+1时：代表左子数组已合并完，因此添加右子数组当前元素tmp[j],并执行j=j+1;
否则，当j=r+1时：代表右子数组已合并完，因此添加左子数组当前元素 tmp[i],并执行i=i+1;
否则，当tmp[i]<=tmp[j]时：添加左子数组当前元素tmp[i],并执行i=i+1;
否则(即tmp[i] > tmp[j])时：添加右子数组当前元素tmp[j],并执行j=j+1;此时构成m-i+1个逆序对，统计添加至res;

4，返回值：res

reversePairs()函数：

1，初始化：辅助数组tmp,用于合并阶段暂存元素；

2，返回值：执行归并排序，并返回逆序对总数；

时间复杂度：O(Nlog N)

空间复杂度：O(N)

class Solution {
public:
    int reversePairs(vector<int>& nums) {
        vector<int>tmp(nums.size());
        return merge_sort(0,nums.size()-1,nums,tmp);
    }
private:
    int merge_sort(int l,int r,vector<int>& nums,vector<int>& tmp){
        //终止条件
        if(l>=r) return 0;
        //递归划分
        int m = (l+r)/2;
        //分成两份后结果分别相加
        int res = merge_sort(l,m,nums,tmp) + merge_sort(m+1,r,nums,tmp); 
        //合并阶段
        int i = l,j=m+1;
        //用一个数组保存合并之前的模样
        for(int k=l;k<=r;k++){
            tmp[k] = nums[k];
        }
        for(int k=l;k<=r;k++){
            //m及其左边元素合并完，把右边剩下的放在合并后的数组
            if(i==m+1) nums[k]=tmp[j++];
            //m+1及其右边元素合并完毕，把左边剩下的放入合并后的数组 或者 左边数组的元素小于等于右边，
            //将左边数组的元素放入结果数组中，并让索引i+1
            else if(j==r+1 || tmp[i]<=tmp[j]) nums[k]=tmp[i++];
            //右边数组的元素小于左边,将右边数组的元素其放入结果数组中,并让索引j加1
            //并且此时左边数组中的从i到m的所有数都是大于tmp[j]的(因为m左右的数组都是已经排好序的，第15行代码的功劳)
            //即此时有m-i+1个逆序对，加到res上即可
            else{
                nums[k]=tmp[j++];
                res += m-i+1;   //统计逆序对
            }
        }
        return res;
    }
};

53 - I. 在排序数组中查找数字 I

统计一个数字在排序数组中出现的次数。

示例：

输入: nums = [5,7,7,8,8,10], target = 8
输出: 2

思路：

方法一：哈希表

class Solution {
public:
    int search(vector<int>& nums, int target) {
        map<int,int> mp;
        for(int i=0;i<nums.size();i++){
            mp[nums[i]]++;
        }
        return mp[target];
    }
};

方法二：二次二分

寻找左边界left和右边界right,数量为right-left-1

算法流程：

1，初始化：左边界i=0,右边界j=len-1

2，循环二分：当闭区间[i,j]无元素时跳出

计算m=(i+j)/2
若nums[m] < target，则target在闭区间[m+1,j]中，执行i=m+1
若nums[m] > target，则target在闭区间[i,m-1]中，执行j=m-1
若nums[m] = target，则右边界right在[m+1,j]中，左边界left在[i,m-1]中，因此分两种情况：
- 若查找right，则执行i=m+!;(跳出时i指向右边界)
- 若查找left，则执行j=m-1;(跳出时j指向左边界)

3，返回值：right-left-1

==以上可以优化为都查找右边界==

查找target的右边界
查找target-1的右边界

时间复杂度O(logN)

空间复杂度O(1)

class Solution {
public:
    int search(vector<int>& nums, int target) {
        return helper(nums,target) - helper(nums,target-1);
    }
    int helper(vector<int>& nums,int tar){
        int i=0,j=nums.size()-1;
        //这边是“小于等于”，因此当循环结束后，ij不重合，且如果存在target值的话，
        //i的位置就是右边界（target值序列右边第一个大于target值的位置），因为最后一次循环一定是i=mid+1；
        //且此时j指向target
        while(i<=j){
            int m=(i+j)/1;
            //这里是“小于等于”，目的是为了确定右边界，就是说当mid等于target时，因为不确定后面还有没有target，所以同样需要左边收缩范围
            if(nums[m] <= tar) i = m + 1;
            else j = m - 1;
        }
        return i;
    }
};

53 - II. 0～n-1中缺失的数字

一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

示例：

输入: [0,1,3] 输出: 2

思路：

方法一：数学或者直接判断

nums[i] 是否等于i

方法二：二分查找

方法三：二分查找

排序数组中的搜索问题，首先想到二分法

左子数组：nums[i]=i

右子数组：nums[i]!=i

算法流程：

1，初始化：左边界i=0,右边界j=len-1;代表区间[i,j]

2，循环二分：当i<=j时循环

计算中点m=(i+j)/2
若nums[m]=m，则右子数组的首位元素一定在[m+1,j]中，执行i=m+1;
若nums[m]!=m，则左子数组的末位元素一定在[i,m-1]中，执行j=m-1

3，返回值：跳出时，i和j分别指向右子数组的首位元素和左子数组的末位元素，因此返回i即可

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int i = 0, j = nums.size() - 1;
        while(i<=j){
            int m = (i + j) / 2;
            if(nums[m] == m) i = m + 1;
            else j = m - 1;
        }
        return i;
    }
};

57. 和为s的两个数字

输入一个递增排序的数组和一个数字s，在数组中查找两个数，使得它们的和正好是s。如果有多对数字的和等于s，则输出任意一对即可。

示例：

输入：nums = [2,7,11,15], target = 9 输出：[2,7] 或者 [7,2]

思路：

方法一：哈希表

复杂度为O(N)

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_set<int,int>mp;
        vector<int> res(2,-1);
        for(int i = 0; i < nums.size(); i++){
            if(mp.count(target-nums[i]) > 0){
                res[0] = target - nums[i];
                res[1] = nums[i];
                return res;
            }
            mp.insert(nums[i]);
        }
        return res;
    }
};

方法二：双指针

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int i = 0, j = nums.size() - 1;
        vector<int> res;
        while(i < j){
            int sum = nums[i] + nums[j];
            if(sum < target) i++;
            else if(sum > target) j--;
            else{
                res.push_back(nums[i]);
                res.push_back(nums[j]);
                return res;
            }
        }
        return res;
    }
};

58 - II. 左旋转字符串

字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如，输入字符串"abcdefg"和数字2，该函数将返回左旋转两位得到的结果"cdefgab"。

示例:

输入: s = "abcdefg", k = 2 输出: "cdefgab"

思路：

方法一：借用一个string

时间复杂度O(N)

空间复杂度O(N)

class Solution {
public:
    string reverseLeftWords(string s, int n) {
        int len = s.size();
        string res;
      	//res = s.substr(n,len-1)+s.substr(0,n);
        for(int i=n;i<len;i++){
            res.push_back(s[i]);
        }
        for(int i=0;i<n;i++){
            res.push_back(s[i]);
        }
        return res;
    }
};

方法二：三次翻转

时间复杂度O(N)

空间复杂度O(1)

三次翻转

例如：

s = "abcdefg" k=2

第一次翻转：整体翻转 gfedcba reverse(s.begin(),s.end());

第二次翻转：翻转len-n个 cdefgba reverse(s.begin(),s.end()-n);

第三次翻转：翻转最后n个 cdefgab reverse(s.end()-n,s.end());

class Solution {
public:
    string reverseLeftWords(string s, int n) {
        //整体翻转
        reverse(s.begin(),s.end());
        //翻转len-n个
        reverse(s.begin(),s.end()-n);
        //翻转最后n个
        reverse(s.end()-n,s.end());
        return s;
    }
};

06.从尾到头打印链表

07. 重建二叉树

示例：

思路：dfs

示例：

思路：

方法一：深度优先遍历DFS

方法二：广度优先遍历BFS

示例：

思路：

示例：

思路：

示例：

思路：

示例：

思路：

示例：

思路：

示例：

思路：

示例：

思路：

示例：

思路：

示例：

思路：

示例：

思路：

示例：

思路：

示例1:

思路：

方法一：哈希表

方法二：拼接+拆分

方法一：快排

方法二：基于快速排序的数组划分

方法三：堆

方法：用大小堆

示例：

思路：

算法流程：

示例：

思路：

示例：

思路：

示例：

思路：

示例:

思路：