前缀和数组

发表于 分类于 ， 阅读次数： Waline： 本文字数： 5.3k 阅读时长 ≈ 5 分钟

前缀和技巧适用于快速、频繁地计算一个索引区间内的元素之和。

303. 区域和检索 - 数组不可变

给定一个整数数组 nums，处理以下类型的多个查询:

计算索引 left和right （包含 left 和 right）之间的 nums 元素的和 ，其中 left <= right 实现 NumArray 类：

  • NumArray(int[] nums) 使用数组 nums 初始化对象
  • int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的总和 ，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + ... + nums[right] )

示例：

输入：

["NumArray", "sumRange", "sumRange", "sumRange"]

[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]

输出：

[null, 1, -1, -3]

解释：

NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);

numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)

numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))

numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

思路：

我们如果没有学过前缀和，可以这样写出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class NumArray {
public:
    vector<int> myNums;
    NumArray(vector<int>& nums) {
        myNums = nums;
    }
    
    int sumRange(int left, int right) {
        int res = 0;
        for(int i = left; i <= right; i++){
            res += myNums[i];
        }
        return res;
    }
};

这样，可以达到效果，但是效率很差，因为 sumRange 方法会被频繁调用，而它的时间复杂度是 O(N)，其中 N 代表 nums 数组的长度。

这道题的最优解法是使用前缀和技巧，将 sumRange 函数的时间复杂度降为 O(1)，说白了就是不要在 sumRange 里面用 for 循环，咋整？

核心思路是我们 new 一个新的数组 preSum 出来，preSum[i] 记录 nums[0..i-1] 的累加和，看图 10 = 3 + 5 + 2：

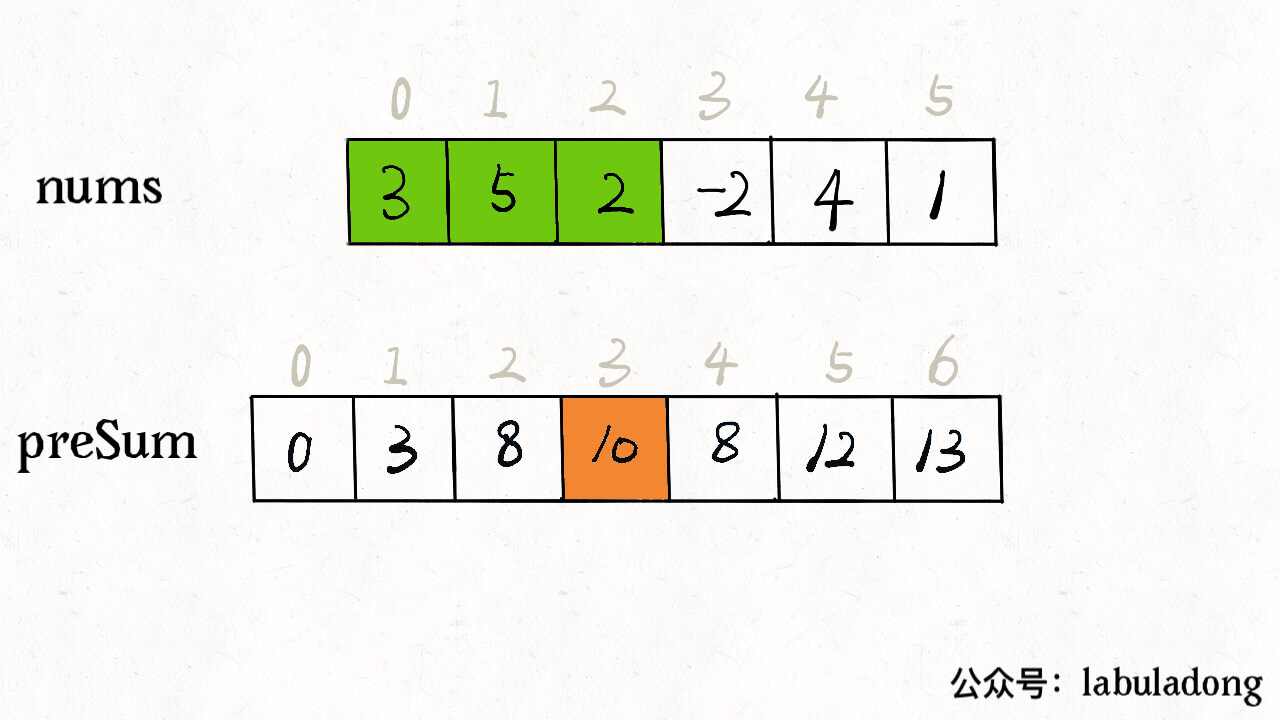
看这个 preSum 数组，如果我想求索引区间 [1, 4] 内的所有元素之和，就可以通过 preSum[5] - preSum[1] 得出。

这样，sumRange 函数仅仅需要做一次减法运算，避免了每次进行 for 循环调用，最坏时间复杂度为常数 O(1)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class NumArray {
public:
    vector<int> preSum;
    NumArray(vector<int>& nums) {
        // preSum[0] = 0, 便于计算累加和
        preSum.resize(nums.size() + 1, 0);
        //计算 nums 的累加和
        for(int i = 1; i < preSum.size(); i++){
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
    }
    
    int sumRange(int left, int right) {
        return preSum[right + 1] - preSum[left];
    }
};

304. 二维区域和检索 - 矩阵不可变

给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。 实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化 int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素总和

示例：

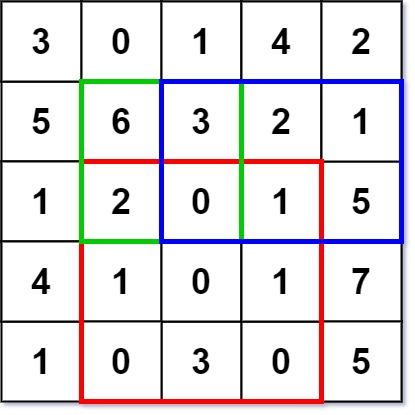
输入:
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出:
[null, 8, 11, 12]

解释: NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

思路：

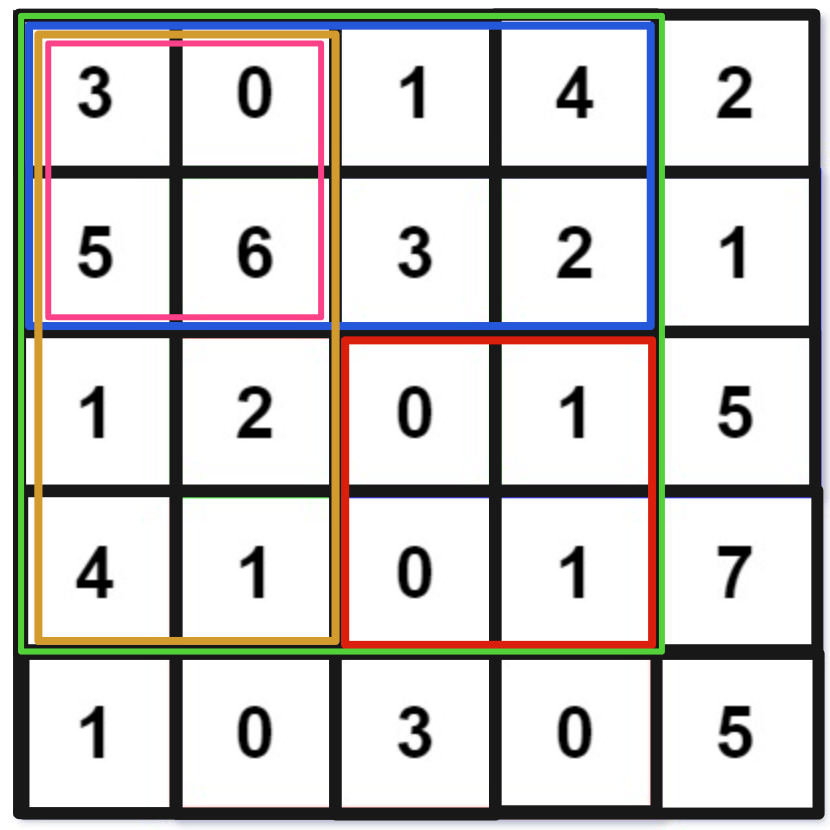
如果我想计算红色的这个子矩阵的元素之和，可以用绿色矩阵减去蓝色矩阵减去橙色矩阵最后加上粉色矩阵，而绿蓝橙粉这四个矩阵有一个共同的特点，就是左上角就是 (0, 0) 原点。

那么我们可以维护一个二维 preSum 数组，专门记录以原点为顶点的矩阵的元素之和，就可以用几次加减运算算出任何一个子矩阵的元素和：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class NumMatrix {
public:
    vector<vector<int> > preSum;
    NumMatrix(vector<vector<int> >& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        if(m == 0 || n == 0) return;
        //构造前缀和矩阵
        preSum.resize(m + 1, vector<int>(n + 1, 0));
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                //计算每个矩阵[0, 0, i, j] 的元素和
                preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] + matrix[i - 1][j - 1] - preSum[i - 1][j - 1];
            }
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        return preSum[row2 + 1][col2 + 1] - preSum[row1][col2 + 1] - preSum[row2 + 1][col1] + preSum[row1][col1];   
    }
};

560. 和为 K 的子数组

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。

示例：

输入：nums = [1,1,1], k = 2
输出：2

输入：nums = [1,2,3], k = 3
输出：2

思路：

方法一：暴力

时机复杂度为O(N^2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int n = nums.size();
        // 构造前缀和
        vector<int> preSum(n + 1, 0);
        preSum[0] = 0;
        for(int i = 0; i < n; i++){
            preSum[i + 1] = preSum[i] + nums[i];
        }

        int res = 0;
        // 穷举所有子数组
        for(int i = 1; i <= n; i++){
            for(int j = 0; j < i; j++){
                // 子数组 nums[j..i-1] 的元素和
                if(preSum[i] - preSum[j] == k){
                    res++;
                }
            }
        }
        return res;
    }
};

方法二：前缀和加哈希表优化

我们针对上一个方法中的穷举所有子数组进行优化

1
2
3
4
5
6
7
8
for(int i = 1; i <= n; i++){
    for(int j = 0; j < i; j++){
      // 子数组 nums[j..i-1] 的元素和
      if(preSum[i] - preSum[j] == k){
          res++;
      }
  }
}

第二层 for 循环在干嘛呢？翻译一下就是，在计算，有几个 j 能够使得 preSum[i] 和 preSum[j] 的差为 k。毎找到一个这样的 j，就把结果加一。

优化的思路是：我直接记录下有几个 preSum[j] 和 preSum[i] - k 相等，直接更新结果，就避免了内层的 for 循环。我们可以用哈希表，在记录前缀和的同时记录该前缀和出现的次数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        // map：前缀和 -> 该前缀和出现的次数
        unordered_map<int, int> preSum;
        preSum[0] = 1;

        int res = 0, pre = 0;
        for(int x : nums){
            pre += x;
            if(preSum.count(pre - k)){
                res += preSum[pre - k];
            }
            preSum[pre]++;
        }
        return res;
    }
};

注意这里我们 preSum 记录的是前缀和到该前缀和出现的次数的映射。

这样，就把时间复杂度降到了 O(N)，是最优解法了。