二叉树

发表于 分类于 ， 阅读次数： Waline： 本文字数： 16k 阅读时长 ≈ 14 分钟

二叉树常用算法

226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例：

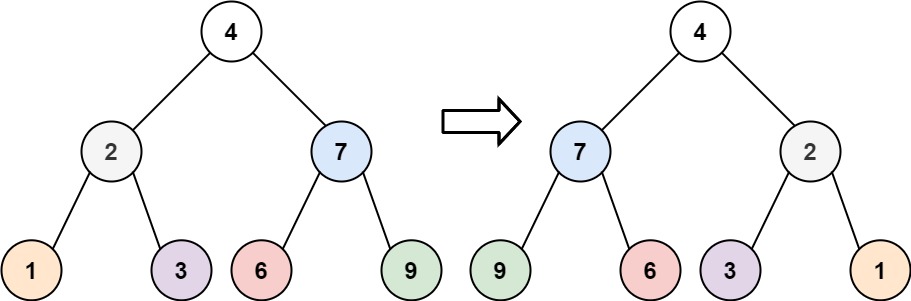
root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

思路：

我们可以发现只需要翻转每个节点的左右子节点。就可以得到翻转后的二叉树了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root == nullptr) return nullptr;

        //交换root节点的左右子节点
        TreeNode* tmp = root->left;
        root->left = root->right;
        root->right = tmp;

        //让左右子节点继续翻转他们的子节点
        invertTree(root->left);
        invertTree(root->right);

        return root;
    }
};

116.填充每个节点的下一个右侧节点指针

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

1
2
3
4
5
6
struct Node {
    int val;
    Node *left;
    Node *right;
    Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例：

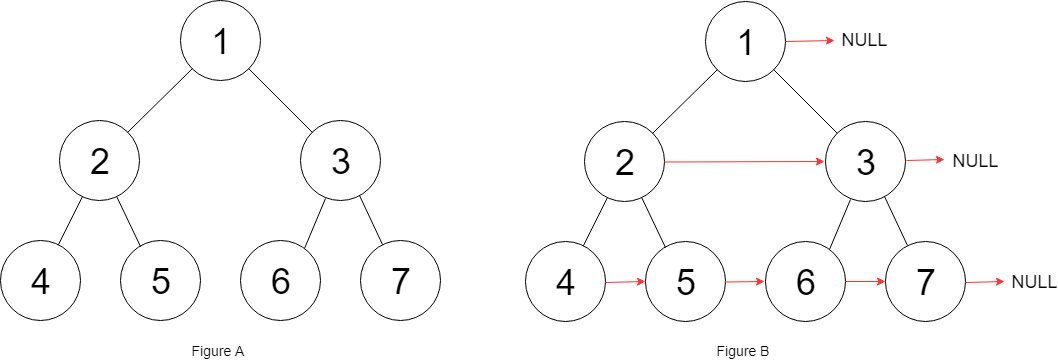
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

思路：

我们可以很轻松的用递归实现左子节点指向右子节点，可是面临一个难题，那就是不同子树的节点，

我们应该如何连接呢？

二叉树的问题难点在于，如何把题目要求细化成每个节点需要做的事。

如果只依赖一个节点的话，我们肯定没有办法连接跨父节点的两个相邻节点，那么我们的做法就是增加函数参数，

使用两个节点。

例如：题中的5和6如何相连，我们只需要递归实现connectTowNode(2->right,3->left)即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    Node* connect(Node* root) {
        if(root == nullptr) return nullptr;
        connectTwoNode(root->left, root->right);
        return root;
    }
    void connectTwoNode(Node* node1, Node* node2){
        if(node1 == nullptr || node2 == nullptr) return;
				
      	//前序位置
        //将传入的节点连接
        node1->next = node2;

        //连接相同父节点的两个节点
        connectTwoNode(node1->left, node1->right);
        connectTwoNode(node2->left, node2->right);

        //连接跨父节点的两个节点
        connectTwoNode(node1->right, node2->left);
    }
};

114. 二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

  • 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
  • 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例：

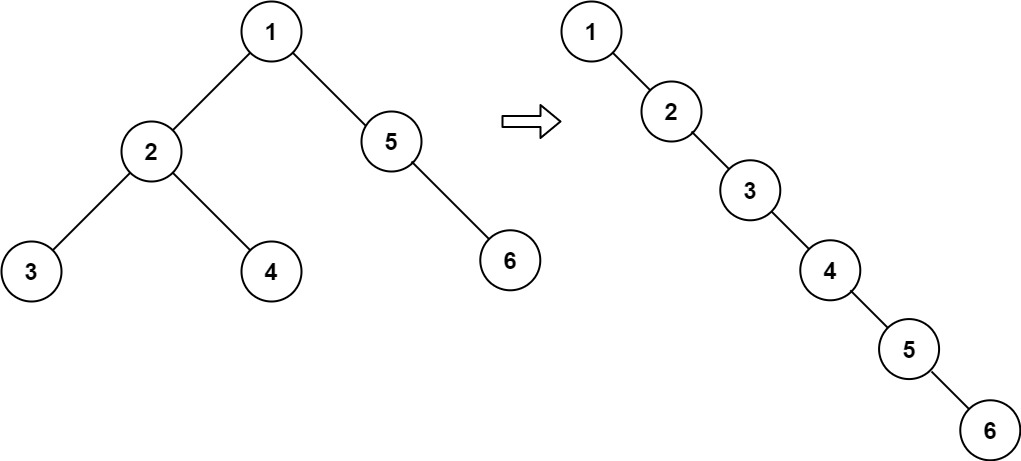
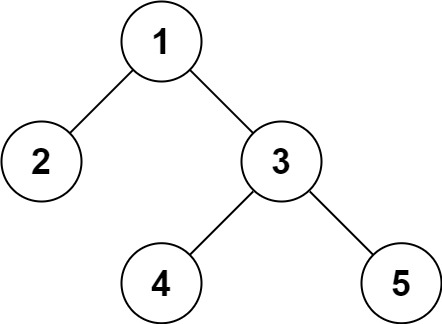
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

思路：

1，将root的左右子树拉平。

2，将root的左子树作为右子树

3，将右子树接到左子树下方

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    void flatten(TreeNode* root) {
        if(root == nullptr) return;

        flatten(root->left);
        flatten(root->right);

        //后续遍历位置，因为我们需要拉平才能操作
        //1，左右子树已经拉平成一条链表
        TreeNode* left = root->left;
        TreeNode* right = root->right;

        //2，将左子树作为右子树
        root->right = left;
        root->left = nullptr;

        //3，将右子树接到左子树下方
        TreeNode* p = root;
        //让p指针指向最末端
        while(p->right != nullptr){
            p = p->right;
        }
        //指向原来的右子树
        p->right = right;
    }
};

654. 最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

  1. 创建一个根节点，其值为 nums 中的最大值。
  2. 递归地在最大值 左边 的 子数组前缀上 构建左子树。
  3. 递归地在最大值 右边 的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

示例：

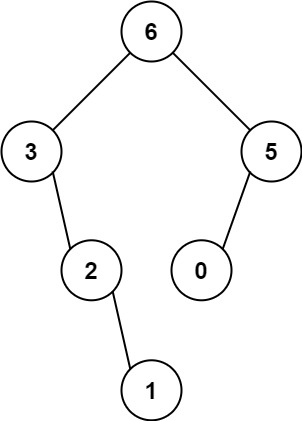
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。 - 空数组，无子节点。 - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。 - 空数组，无子节点。 - 只有一个元素，所以子节点是一个值为 1 的节点。 - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。 - 只有一个元素，所以子节点是一个值为 0 的节点。 - 空数组，无子节点。

思路：

我们首先要明确每个节点应该做什么？很显然每个节点要做的就是把自己构造出来

  1. 递归终止条件lo > hi

  2. 遍历找出最大值maxVal

  3. 递归左右两边作为左右子树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        if(nums.empty()) return nullptr;
        return build(nums, 0, nums.size() - 1);
    }
    TreeNode* build(vector<int>& nums, int lo, int hi){
        //递归终止条件
        if(lo > hi) return nullptr;

        //找到数组中最大值和对应的索引
        int index = -1, maxVal = INT_MIN;
        for(int i = lo; i <= hi; i++){
            if(maxVal < nums[i]){
                index = i;
                maxVal = nums[i];
            }
        }

        //构建自己的节点
        TreeNode* root = new TreeNode(maxVal);
        //递归构建自己节点的左右子树
        root->left = build(nums, lo, index-1);
        root->right = build(nums, index + 1, hi);

        return root;
    }
};

105. 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例：

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

1
2
3
4
5
6
7
8
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
思路：

我们主要的就是把根节点做出来，然后递归构造左右子树即可。

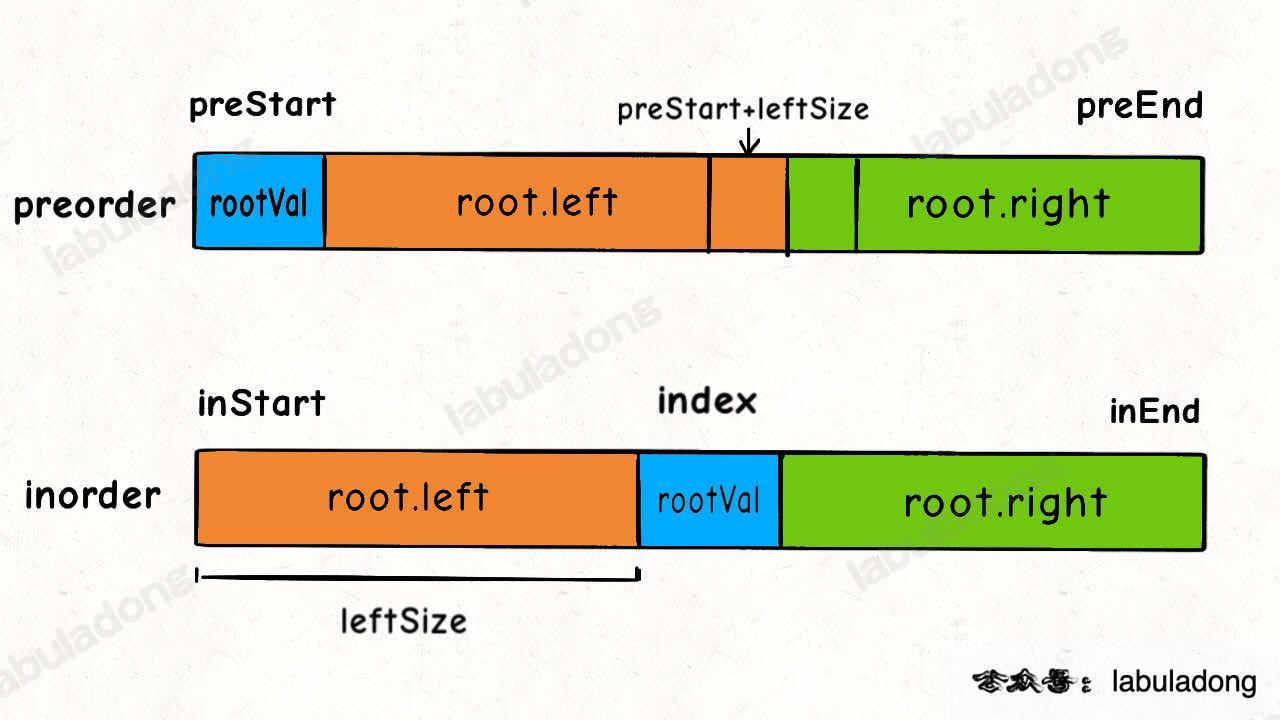
前序遍历可以把数组分成[根，左， 右]三部分，而中序遍历可以把数组分为[左，根， 右]三部分

我们知道前序遍历的第一个值就是根节点的值，关键在于如何通过根节点的值。将preorder和inorder分为两半，构建根节点的左右子树

这样就可以分为：

1
2
3
int leftSize = index - inStart;
root->left = build(preorder, preStart + 1, preStart + leftSize, inorder, inStart, index - 1);
root->right = build(preorder, preStart + leftSize + 1, preEnd, inorder, index + 1, inEnd);

综上：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        //前序，前序起点，前序终点，中序，中序起点，中序终点
        return build(preorder, 0, preorder.size() - 1, inorder, 0, inorder.size() - 1);
    }
    TreeNode* build(vector<int>& preorder, int preStart, int preEnd, vector<int>& inorder, int inStart, int inEnd){
        //递归终止条件
        if(preStart > preEnd) return nullptr;
        //root 节点就是前序遍历的第一个节点
        int rootVal = preorder[preStart];
        //rootVal 在中序遍历中的索引
        int index = 0;
        for(int i = inStart; i <= inEnd; i++){
            if(inorder[i] == rootVal){
                index = i;
                break;
            }
        }
        //左子树长度
        int leftSize = index - inStart;
        //构建根节点
        TreeNode* root = new TreeNode(rootVal);
        //递归构建左右子树
        root->left = build(preorder, preStart + 1, preStart + leftSize, inorder, inStart, index - 1);
        root->right = build(preorder, preStart + leftSize + 1, preEnd, inorder, index + 1, inEnd);

        return root;
    }
};

106. 从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例：

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

思路：

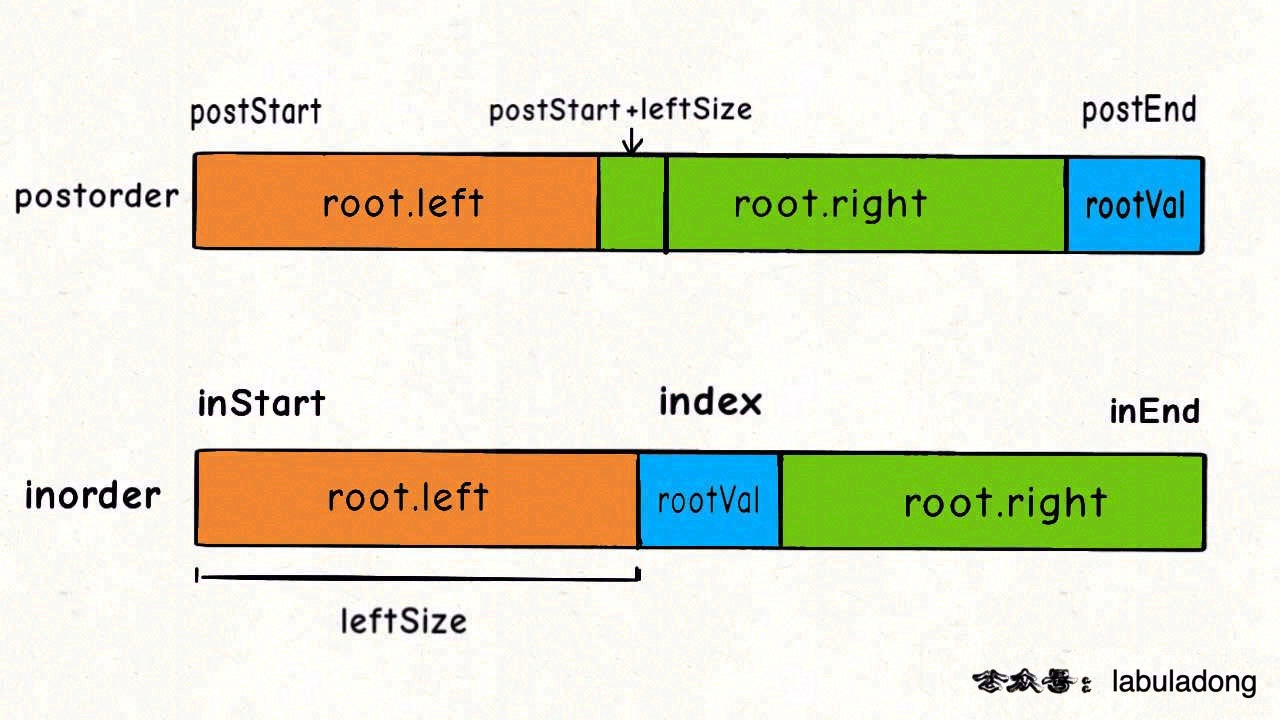
和上题一样，我们只需要知道后序遍历为[左 右 根]根节点为最后一个元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return build(inorder, 0, inorder.size() - 1, postorder, 0, postorder.size() - 1);
    }
    TreeNode* build(vector<int>& inorder, int inStart, int inEnd, vector<int>& postorder, int postStart, int postEnd){
        //递归终止条件
        if(inStart > inEnd) return nullptr;
        //root 为后序遍历postorder的最后一个节点
        int rootVal = postorder[postEnd];
        //rootVal 在中序遍历中的索引
        int index = 0;
        for(int i = inStart; i <= inEnd; i++){
            if(inorder[i] == rootVal){
                index = i;
                break;
            }
        }
        //计算左子树长度
        int leftSize = index - inStart;
        //构建根节点
        TreeNode* root = new TreeNode(rootVal);
        //递归构建左右子树
        root->left = build(inorder, inStart, index - 1, postorder, postStart, postStart + leftSize - 1);
        root->right = build(inorder, index + 1, inEnd, postorder, postStart + leftSize, postEnd - 1);

        return root;
    }
};

889. 根据前序和后序遍历构造二叉树

给定两个整数数组，preorder 和 postorder ，其中 preorder 是一个具有 无重复 值的二叉树的前序遍历，postorder 是同一棵树的后序遍历，重构并返回二叉树。

如果存在多个答案，您可以返回其中 任何 一个。

示例：

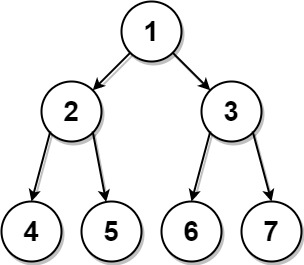
输入：preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1]
输出：[1,2,3,4,5,6,7]

1
2
3
4
5
6
7
8
9
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

思路：

通过前序中序，或者后序中序遍历可以确定一棵原始二叉树，但是通过前序后序结果无法确定原始二叉树。

1，首先把前序遍历的第一个节点或者后序遍历的最后一个元素作为根节点的值

2，然后把前序遍历结果的第二个元素作为左子树的根节点的值

3，在后序遍历结果中寻找左子树根节点的值，从而确定了左子树的索引边界，进而确定右子树的索引边界，递归构造左右子树即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    TreeNode* constructFromPrePost(vector<int>& preorder, vector<int>& postorder) {
        return build(preorder, 0, preorder.size() - 1, postorder, 0, postorder.size() - 1);
    }
    TreeNode* build(vector<int>& preorder, int preStart, int preEnd, vector<int>& postorder, int postStart, int postEnd){
        //递归终止条件
        if(preStart > preEnd) return nullptr;
        //只剩一个节点了，直接构建为新节点即可
        if(preStart == preEnd) return new TreeNode(preorder[preStart]);
        //root 为前序遍历的第一个元素
        int rootVal = preorder[preStart];
        //leftRoot 为前序遍历的第二个元素
        //通过前序和后序遍历构造二叉树的关键在于通过左子树
        //确定preorder 和 postorder 中左右子树的元素区间
        int leftRootVal = preorder[preStart + 1];
        //leftRootVal 在后序遍历数组中的索引
        int index = 0;
        //这里不能等于，因为相等时,就没有leftRootVal了
        for(int i = postStart; i < postEnd; i++){
            if(postorder[i] == leftRootVal){
                index = i;
                break;
            }
        }
        // 左子树长度，记得加一，因为 index 也属于左子树
        int leftSize = index - postStart + 1;

        //先构建出当前根节点
        TreeNode* root = new TreeNode(rootVal);
        //递归构建左右子树
        root->left = build(preorder, preStart + 1, preStart + leftSize, postorder, postStart, index);
        root->right = build(preorder, preStart + leftSize + 1, preEnd, postorder, index + 1, postEnd - 1);

        return root;
    }
};

652. 寻找重复的子树

给定一棵二叉树 root，返回所有重复的子树。

对于同一类的重复子树，你只需要返回其中任意一棵的根结点即可。

如果两棵树具有相同的结构和相同的结点值，则它们是重复的。

示例：

输入：root = [1,2,3,4,null,2,4,null,null,4]
输出：[[2,4],[4]]

思路：

具体请点击

对于某一点，它应该做什么？

1，以我为根的这颗二叉树长什么样？

2，以其他节点为根的子树都长什么样？

可以看出我们可以选择「后序遍历」框架来解决：

1
2
3
4
5
void traverse(TreeNode* root){
	traverse(root->left);
	traverse(root->right);
	/*解法代码位置*/
}

因为我要知道以自己为根的子树长什么样，是不是得先知道我的左右子树长什么样，再加上自己，就构成了整颗子树的样子。

那么接下来我们应该怎么描述一棵二叉树的模样呢？

通过二叉树序列化：通过拼接字符串的方式。

1
2
3
4
5
6
7
8
9
10
11
string traverse(TreeNode* root){
	//对于空节点，可以用一个特殊字符表示
	if(root == null) return '#';
	//将左右子树序列化成字符串
	string left = traverse(root->left);
	string right = traverse(root->right);
	/*后序遍历位置*/
	//左右子树加上自己，就是以自己为根的二叉树序列化结果
	string subTree = left + "," + right + "," + to_string(root->val);
	return subTree;
}

这样我们解决了第一个问题，知道了自己长什么样，现在解决第二个问题，怎么知道别人长什么样？这样我才能知道有没有其他子树根我重复。

我们只需要借助unordered_map，让每个节点把自己子树的序列化结果存进去，这样，对于每个节点，不就知道有没有其他节点的子树和自己重复了。

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    // 记录所有子树以及出现的次数
    unordered_map<string, int> mp;
    vector<TreeNode*> res;
    vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {
        traverse(root);
        return res;
    }
    string traverse(TreeNode* root){
        //递归终止条件
        if(root == nullptr){
            return "#";
        }
        //二叉树序列化
        string left = traverse(root->left);
        string right = traverse(root->right);
        string subTree = left + "," + right + "," + to_string(root->val);

        if(mp[subTree] == 1){
            res.push_back(root);
        }
        //给子树对应的出现次数加一
        mp[subTree]++;
        return subTree;
    }
};

297. 二叉树的序列化与反序列化

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

提示: 输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

示例:

输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]

思路：

先序实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Codec {
public:

    // 将二叉树转化为字符串
    string serialize(TreeNode* root) {
        string res;
        mySerialize(root,res);
        return res;
    }
    // 辅助函数，将二叉树存入 str
    void mySerialize(TreeNode* root, string& str){
        if(root == nullptr){
            str += "#,";
        }else{
            //前序遍历
            str += to_string(root->val) + ",";
            mySerialize(root->left, str);
            mySerialize(root->right, str);
        }
    }

    // 将字符串反序列化为二叉树结构
    TreeNode* deserialize(string data) {
        string str;
        //将字符串反序列化为列表
        list<string> datalist;
        for(auto& ch : data){
            if( ch == ','){
                datalist.push_back(str);
                //删除容器存储的所有元素
                str.clear();
            }else{
                str.push_back(ch);
            }
        }
        if(!str.empty()){
            datalist.push_back(str);
            str.clear();
        }
        return myDeserialize(datalist);
    }
    //辅助函数，通过 nodes 列表构造二叉树
    TreeNode* myDeserialize(list<string>& datalist){
        if(datalist.front() == "#"){
            datalist.erase(datalist.begin());
            return nullptr;
        }
        // 列表最左侧就是根节点
        TreeNode* root = new TreeNode(stoi(datalist.front()));
        datalist.erase(datalist.begin());
        root->left = myDeserialize(datalist);
        root->right = myDeserialize(datalist);
        return root;
    }
};

1373. 二叉搜索子树的最大键值和

给你一棵以 root 为根的 二叉树 ，请你返回 任意 二叉搜索子树的最大键值和。

二叉搜索树的定义如下：

  • 任意节点的左子树中的键值都 小于 此节点的键值。

  • 任意节点的右子树中的键值都 大于 此节点的键值。

  • 任意节点的左子树和右子树都是二叉搜索树。

示例：

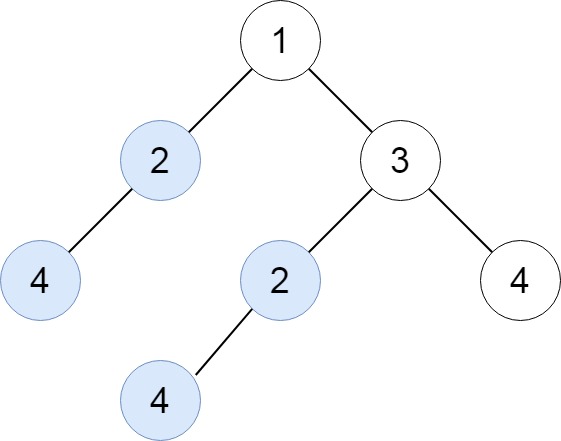
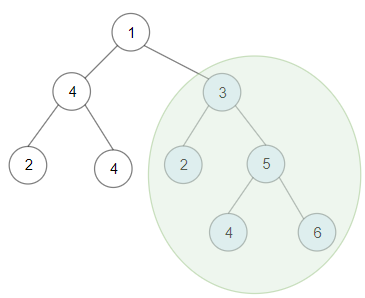
输入：root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
输出：20
解释：键值为 3 的子树是和最大的二叉搜索树。

思路：

1，左右子树是不是BST

2，左子树的最大值和右子树的最小值

3，左右子树的节点值之和

traverse(root)返回一个大小为4的int数组res

res[0] 记录以 root 为根的二叉树是否是BST，若为1则说明是BST，否则不是

res[1] 记录以 root 为根的二叉树所有节点中的最小值；

res[2] 记录以 root 为根的二叉树所有节点中的最大值；

res[3] 记录以 root 为根的二叉树所有节点值之和；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
public:
    int maxSum = 0;
    int maxSumBST(TreeNode* root) {
        traverse(root);
        return maxSum;
    }
    vector<int> traverse(TreeNode* root){
        //递归终止条件
        vector<int> tmp = {1,INT_MAX,INT_MIN,0};
        if(root == nullptr){
            return tmp;
        }

        // 递归计算左右子树
        vector<int> left(4);
        vector<int> right(4);
        left = traverse(root->left);
        right = traverse(root->right);

        //后序遍历位置
        vector<int> res(4);
        // if 判断以 root 为根的二叉树是不是BST
        if(left[0] == 1 && right[0] == 1 && root->val > left[2] && root->val < right[1]){
            res[0] = 1;
            //计算以 root 为根的这颗 BST 的最小值
            res[1] = min(left[1],root->val);
            //计算以 root 为根的这颗 BST 的最大值
            res[2] = max(right[2],root->val);
            //计算以 root 为根的这颗 BST 所有节点之和
            res[3] = left[3] + right[3] + root->val;
            //更新全局变量
            maxSum = max(maxSum, res[3]);
        }else{
            //以 root 为根的二叉树不是 BST
            res[0] = 0;
            //其他值就不需要计算了
        }
        return res;
    }
};