单词接龙

发表于 更新于 分类于 ， 阅读次数： Waline： 本文字数： 3.2k 阅读时长 ≈ 3 分钟

P1019

题目描述

单词接龙是一个与我们经常玩的成语接龙相类似的游戏，现在我们已知一组单词，且给定一个开头的字母，要求出以这个字母开头的最长的“龙”（每个单词都最多在“龙”中出现两次），在两个单词相连时，其重合部分合为一部分，例如 beast和astonish，如果接成一条龙则变为beastonish，另外相邻的两部分不能存在包含关系，例如at和 atide 间不能相连。

输入输出格式

输入格式：

输入的第一行为一个单独的整数n (n≤20)表示单词数，以下n 行每行有一个单词，输入的最后一行为一个单个字符，表示“龙”开头的字母。你可以假定以此字母开头的“龙”一定存在.

输出格式：

只需输出以此字母开头的最长的“龙”的长度

输入样例：

5
at
touch
cheat
choose
tact
a

输出样例：

23

说明：

连成的龙为atoucheatactactouchoose.

解题思路：

把它转化成二叉树，然后dfs就可以了

具体方式如下（不全，注意思想就好了）:

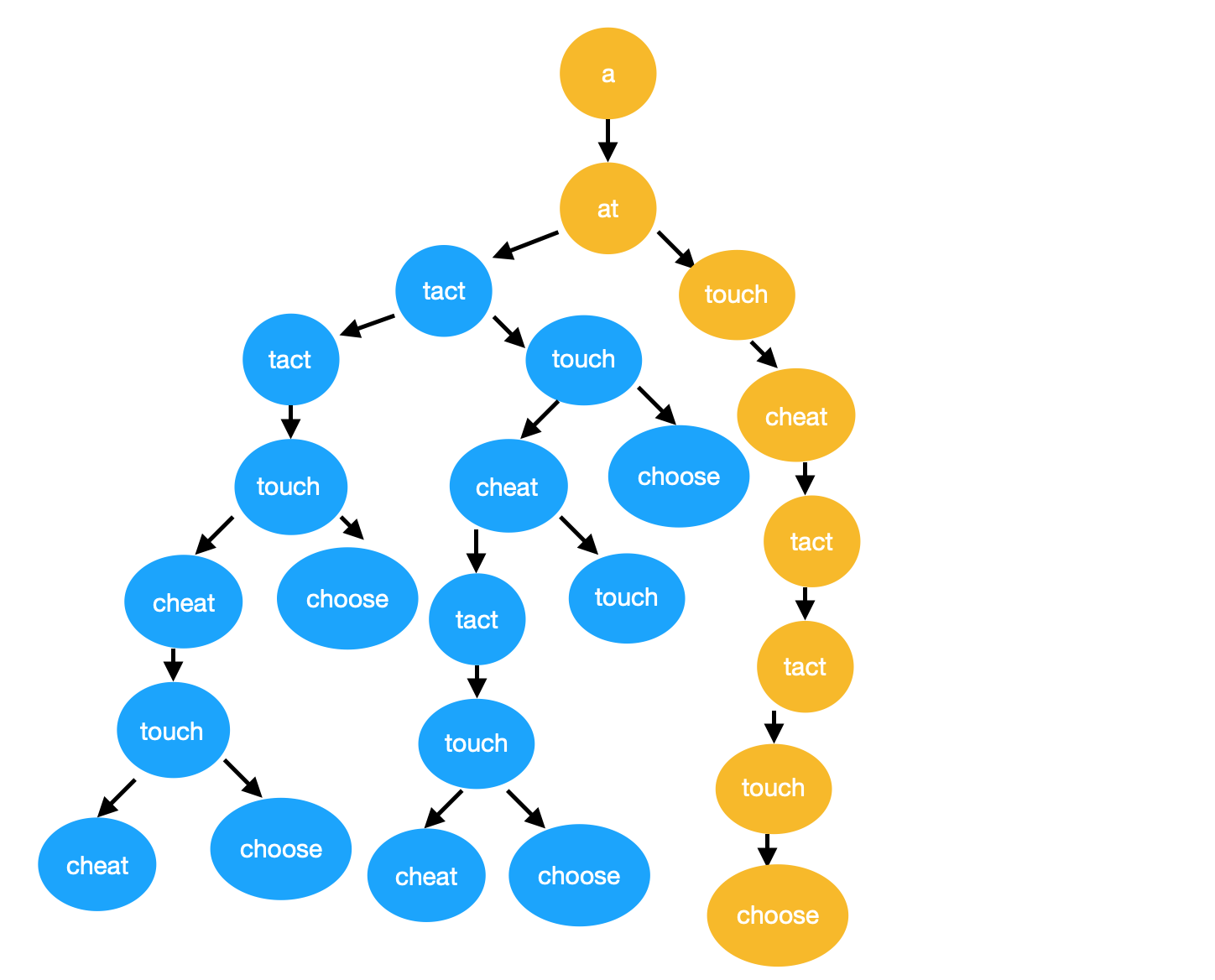dfs

黄色部分就是最长的了。

这道题最关键的不是dfs，而是我们如何找到下一步要接龙的头。也就是要如何找到两个单词最小重叠部分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int min_cover_word(int x,int y)//x表示当前单词，y表示下一个要接龙的单词
{
    bool p=true;
    int y_start=0;//单词y开始搜索位置
    for(int k=str[x].size()-1;k>=0;k--){
        for(int x_start=k; x_start<str[x].size();x_start++){//x_start为单词x开始搜索位置
            if(str[x][x_start] != str[y][y_start++]){//不等时直接退出
                p=false;
                break;
            }
        }
        if(p==true) return str[x].size()-k;//得到最小重叠长度
        y_start=0;
        p=true;
    }
    return 0;
}

这步可能不太容易理解，可以在草稿中模拟一下就清楚了。

AC代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <iostream>
#include <cstring>
#include <cmath>
#include <cstdio>
#include <algorithm>
#include <vector>
#define ll long long
using namespace std;

string str[100];//储存单词
int vis[100];//判断单词的使用次数
int n,ans=-1,now=0;//now每次搜到的f当前最长串
int min_cover[100][100];//两个单词最小重叠部分
char ch;//龙头

int min_cover_word(int x,int y)
{
    bool p=true;
    int y_start=0;//单词y开始搜索位置
    for(int k=str[x].size()-1;k>=0;k--){
        for(int x_start=k; x_start<str[x].size();x_start++){//x_start为单词x开始搜索位置
            if(str[x][x_start] != str[y][y_start++]){//不等时直接退出
                p=false;
                break;
            }
        }
        if(p==true) return str[x].size()-k;//得到最小重叠长度
        y_start=0;
        p=true;
    }
    return 0;
}

void dfs(int x)
{
    bool jx=false;
    for(int i=1;i<=n;i++){
        if(vis[i]>=2) continue;//使用了2次就跳过
        if(min_cover[x][i]==0) continue;//两个单词没有重合b部分，跳过
        if(min_cover[x][i]==str[x].size() || min_cover[x][i] == str[i].size()) continue;//两者存在包含关系，跳过
        
        now += str[i].size()-min_cover[x][i];//两单词合并然后减去重叠部分的长度
        vis[i]++;//使用次数增加
        jx=true;//标志当前已经成功匹配到一个可以连接的部分
        dfs(i);//继续合并
        now -= str[i].size()-min_cover[x][i];//回溯,返回到上一步的状态
        vis[i]--;//回溯
    }
    if(jx==false) ans=max(ans,now);//n表示已经不能找到可以连接到单词,更新长度
    return;
}

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>str[i];
    cin>>ch;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            min_cover[i][j]=min_cover_word(i,j);
        }
    }
    //预处理min_cover数组。min_cover[i][j]就表示，i单词后连接一个j单词的最小重叠部分
    //比如 i表示at,j表示att. min_cover[i][j]就为2 但是min_cover[j][i]就为0.
    //预处理是一个关键
    for(int i=1;i<=n;i++){
        if(str[i][0]==ch){//找到和首字母和龙头匹配的单词
            vis[i]++;//使用次数增加
            now=str[i].size();//更新当前串长度
            dfs(i);//连接
            vis[i]=0;//清除影响
        }
    }
    cout<<ans<<endl;
    return 0;
}