快速排序之所比较快,因为相比冒泡排序,每次交换是跳跃式的。每次排序的时候设置一个基准点,将小于等于基准点的数全部放到基准点的左边,将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换,交换的距离就大的多了。因此总的比较和交换次数就少了,速度自然就提高了。当然在最坏的情况下,仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的都是O(N2),它的平均时间复杂度为O(NlogN)。其实快速排序是基于一种叫做“二分”的思想。我们后面还会遇到“二分”思想。
知道快排的思想后,我们可以看下这道题:
P1309
题目背景
在双人对决的竞技性比赛,如乒乓球、羽毛球、国际象棋中,最常见的赛制是淘汰赛和循环赛。前者的特点是比赛场数少,每场都紧张刺激,但偶然性较高。后者的特点是较为公平,偶然性较低,但比赛过程往往十分冗长。
本题中介绍的瑞士轮赛制,因最早使用于1895年在瑞士举办的国际象棋比赛而得名。它可以看作是淘汰赛与循环赛的折中,既保证了比赛的稳定性,又能使赛程不至于过长。
题目描述
2×N名编号为 1∼2N 的选手共进行R
轮比赛。每轮比赛开始前,以及所有比赛结束后,都会按照总分从高到低对选手进行一次排名。选手的总分为第一轮开始前的初始分数加上已参加过的所有比赛的得分和。总分相同的,约定编号较小的选手排名靠前。
每轮比赛的对阵安排与该轮比赛开始前的排名有关:第1 名和第2 名、第 3
名和第 4名、……、第2K−1名和第2K名、……
、第2N−1名和第2N名,各进行一场比赛。每场比赛胜者得1分,负者得
0分。也就是说除了首轮以外,其它轮比赛的安排均不能事先确定,而是要取决于选手在之前比赛中的表现。
现给定每个选手的初始分数及其实力值,试计算在R 轮比赛过后,排名第Q
的选手编号是多少。我们假设选手的实力值两两不同,且每场比赛中实力值较高的总能获胜。
输入输出格式
输入格式:
第一行是三个正整数N,R,Q,每两个数之间用一个空格隔开,表示有
2×N名选手、R 轮比赛,以及我们关心的名次 Q。
第二行是2×N
个非负整数s1,s2,…,s2N,每两个数之间用一个空格隔开,其中si表示编号为i
的选手的初始分数。 第三行是2×N
个正整数w1,w2,…,w2N,每两个数之间用一个空格隔开,其中 wi 表示编号为i
的选手的实力值。
输出格式:
一个整数,即R轮比赛结束后,排名第Q 的选手的编号。
输入样例:
2 4 2
7 6 6 7
10 5 20 15
输出样例:
1
【数据范围】
对于30%的数据,1≤N≤100;
对于50%的数据,1≤N≤10,000;
对于100%的数据,1≤N≤100,000,1≤R≤50,1≤Q≤2N,0≤s1,s2,…,s2N≤108,1≤w1,w2,…,w2N≤108.
noip2011普及组第3题。
解题思路:
刚开始没注意看范围,以为直接快排就能过,但是TLE了。
后面看了下,发现赢的基本上位置没有发生变化,当然输的相对位置也没有发生变化,
这不就是归并排序吗?
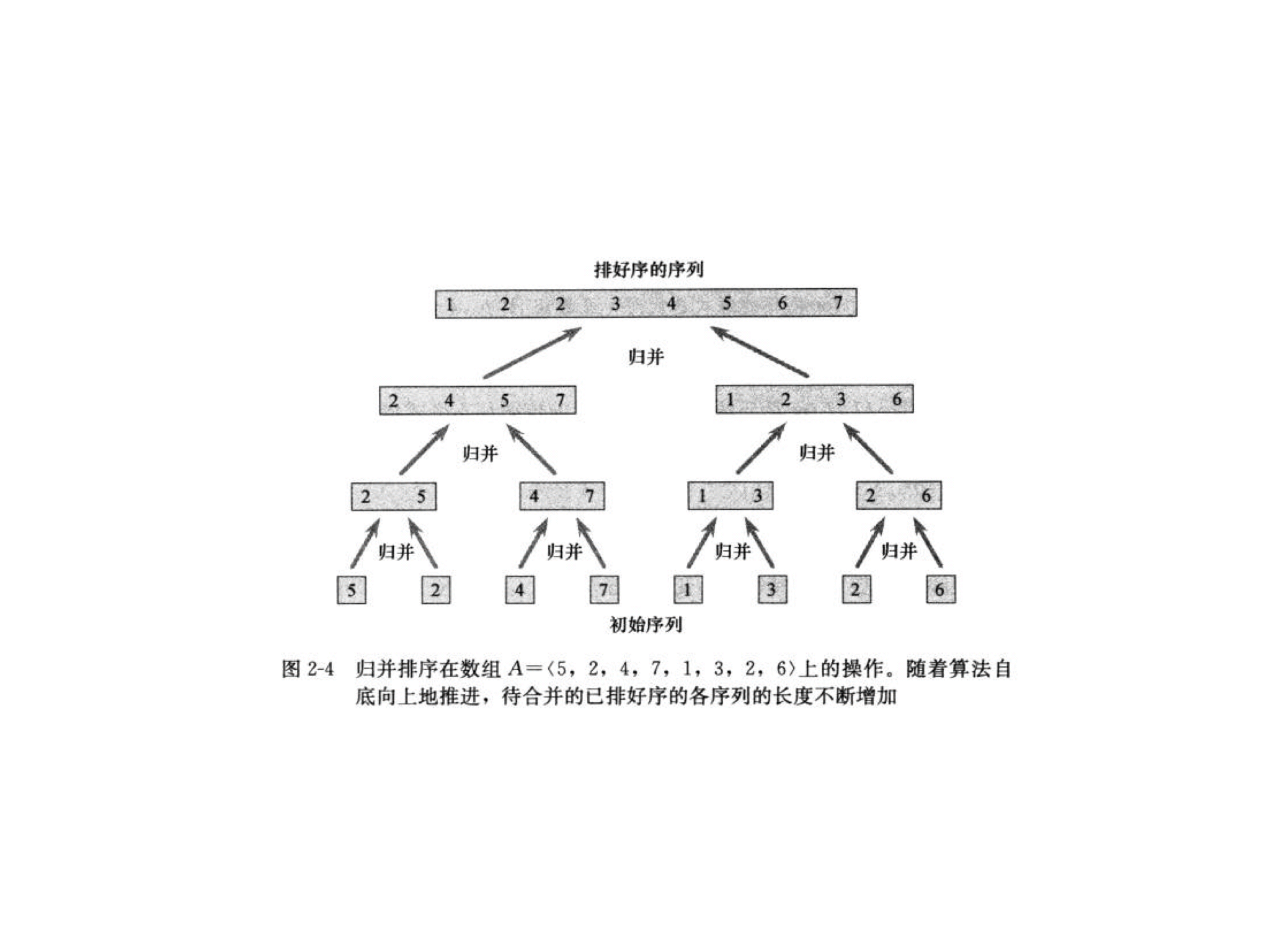
下面先附上TLE的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| #include <iostream>
#include <cstring>
#include <cmath>
#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
struct xs{
ll s,w,id;
}p[200000+10];
bool cmp(const xs &a, const xs &b)
{
if (a.s==b.s) return a.id<b.id;
return a.s>b.s;
}
int main()
{
ll n,r,q;
cin >> n >> r >> q;
for(ll i=0;i<2*n;i++){
p[i].id = i+1;
cin>>p[i].s;
}
for (ll i=0; i<2*n;i++){
cin >> p[i].w;
}
while(r--){
ll j = 0;
for(j=0;j<2*n;j=j+2){
if(p[j].w>p[j+1].w) p[j].s+=1;
else p[j+1].s+=1;
}
sort(p,p+2*n,cmp);
}
cout << p[q-1].id << endl;
return 0;
}
|
下面是归并排序的算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include <iostream>
#include <cstring>
#include <cmath>
#include <cstdio>
#include <algorithm>
#include <queue>
#define ll long long
using namespace std;
ll n,r,q;
struct xs{
ll id;
ll s;
ll w;
} p[200010], a[200010],b[200010];
int cmp(const xs &a, const xs &b)
{
if (a.s==b.s) return a.id<b.id;
return a.s>b.s;
}
int main()
{
cin >> n>>r>>q;
for(int i=1;i<=2*n; i++){
cin>>p[i].s;
p[i].id = i;
}
for(int i=1; i<=2*n;i++){
cin>>p[i].w;
}
sort(p+1,p+2*n+1,cmp);
for(int i=1;i<=r;i++){
int ai=0,bi=0;
for(int j=1;j<=2*n;j = j+2){
if(p[j].w>p[j+1].w){
p[j].s++;
b[++bi]=p[j+1];
a[++ai]=p[j];
}
else {
p[j+1].s++;
b[++bi]=p[j];
a[++ai]=p[j+1];
}
}
merge(a+1,a+n+1,b+1,b+n+1,p+1,cmp);
}
cout << p[q].id << endl;
return 0;
}
|
